Solved Examples and Worksheet for Parallel Lines and Transversals

Q1Find the value of x, if y = 35° and b = 70°.

A. 75°
B. 205°
C. 145°
D. 110°

Solutions
Share 
Step: 1
a + 35° = 70°
  [Alternate Interior Angles Theorem.]
Step: 2
a = 35°
  [Simplify.]
Step: 3
a + x = 180°
  [Same-Side Interior Angles Theorem.]
Step: 4
35° + x = 180°
  [Substitute.]
Step: 5
x = 145°
  [Simplify.]
Correct Answer is :    145°
Q2m∠ECB = 140°, find m∠ABC.


A. 40°
B. 140°
C. 50°
D. 320°

Solutions
Share 
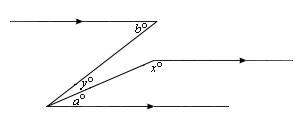
Step: 1
m∠ECD = 180°
  [∠ECD is a straight angle.]
Step: 2
m∠ECB + m∠BCD = 180°
  [Angle Addition Postulate.]
Step: 3
140° + m∠BCD = 180°
  [Substitute.]
Step: 4
m∠BCD = 40°
  [Simplify.]
Step: 5
m∠ABC = m∠BCD
  [Alternate Interior Angles Theorem.]
Step: 6
m∠ABC = 40°
  [Substitute.]
Correct Answer is :   40°
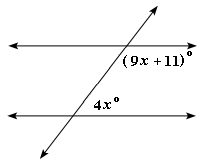
Q3In the following figure, two parallel lines are cut by a transversal. Find x.

A. 13
B. 52
C. 106
D. 117
E. 128

Solutions
Share 
Step: 1
The two labeled angles are supplementary angles and hence their sum is equal to 180o.
Step: 2
4x + 9x + 11 = 180
Step: 3
13x + 11 = 180
Step: 4
13x = 169 ⇒ x = 13
Correct Answer is :   13
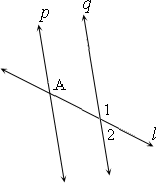
Q4If p and q are parallel and m∠A = 125, find the m∠1 and m∠2.

A. m∠1 = 250 and m∠2 = 62
B. m∠1 = 55 and m∠2 = 125
C. m∠1 = 125 and m∠2 = 55
D. m∠1 = 235 and m∠2 = 125

Solutions
Share 
Step: 1
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
  [Corresponding angles postulate.]
Step: 2
∠1 = 125°
  [Corresponding angles.]
Step: 3
∠1 + ∠2 = 180°
  [Linear Pair.]
Step: 4
125° + ∠2 = 180°
Step: 5
∠2 = 180°- 125°
Step: 6
∠2 = 55°
Step: 7
Hence m∠1 = 125 and m∠2 = 55
Correct Answer is :   m∠1 = 125 and m∠2 = 55
Q5Find the value of x.


A. 140
B. 120
C. 110
D. 60
E. 100

Solutions
Share 
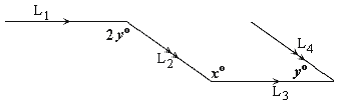
Step: 1
From the figure, x° = 2y° ⇒ 12x° = y°
  [Alternate angles.]
Step: 2
From the figure, x° + y° = 180°
  [Supplementary angles.]
Step: 3
x° + y° = 180° ⇒ x° + 12x° = 180°
  [From step 1 and step 2.]
Step: 4
⇒ x° = 120°.
  [Solve for x.]
Correct Answer is :   120
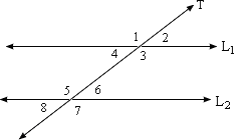
Q6Two parallel lines L1 and L2 are cut by a transversal T. Use the figure to find how are ∠4 and ∠5 related.


A. complementary.
B. congruent.
C. supplementary.
D. none of the above

Solutions
Share 
Step: 1
∠4 + ∠5 = 180o
  [Same-Side Interior Angles Theorem.]
Step: 2
∠4 and ∠5 are Supplementary.
  [Step 1.]
Correct Answer is :   supplementary.
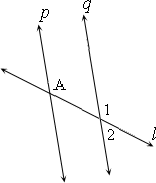
Q7Find the measures of ∠1 and ∠2, if m∠A equals 135.

A. m∠1 = 45 and m∠2 = 135
B. m∠1 = 270 and m∠2 = 67
C. m∠1 = 225 and m∠2 = 135
D. m∠1 = 135 and m∠2 = 45

Solutions
Share 
Step: 1
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
  [Corresponding angles postulate.]
Step: 2
∠1 = 135°
  [Corresponding angles.]
Step: 3
∠1 + ∠2 = 180°
  [Adjacent angles.]
Step: 4
135° + ∠2 = 180°
Step: 5
∠2 = 180°- 135°
Step: 6
∠2 = 45°
Step: 7
Hence m∠1 = 135 and m∠2 = 45
Correct Answer is :   m∠1 = 135 and m∠2 = 45
Q8m∠ECB = 130, find m∠ABC.

A. 310
B. 130
C. 50
D. 40

Solutions
Share 
Step: 1
m∠ECD = 180
  [∠ECD is a straight angle.]
Step: 2
m∠ECB + m∠BCD = 180
  [Angle Addition Postulate.]
Step: 3
130 + m∠BCD = 180
  [Substitute.]
Step: 4
m∠BCD = 50
  [Simplify.]
Step: 5
m∠ABC = m∠BCD
  [Alternate Interior Angles Theorem.]
Step: 6
m∠ABC = 50
  [Substitute.]
Correct Answer is :   50
Q9Find the value of x.


A. 90°
B. 30°
C. 60°
D. 45°

Solutions
Share 
Step: 1
In a parallelogram adjacent angles are supplementary .
Step: 2
x + 3x = 180°
  [Adjacent angles.]
Step: 3
4x = 180° ⇒ x = 45°
  [Simplify.]
Correct Answer is :   45°
Q10m∠ECB = 160, find m∠ABC.

A. 340
B. 160
C. 20
D. 115

Solutions
Share 
Step: 1
m∠ECD = 180
  [∠ECD is a straight angle.]
Step: 2
m∠ECB + m∠BCD = 180
  [Angle Addition Postulate.]
Step: 3
160 + m∠BCD = 180
  [Substitute.]
Step: 4
m∠BCD = 20
  [Simplify.]
Step: 5
m∠ABC = m∠BCD
  [Alternate Interior Angles Theorem.]
Step: 6
m∠ABC = 20
  [Substitute.]
Correct Answer is :   20
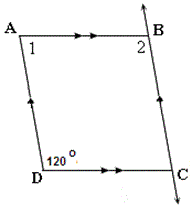
Q11Find the m∠1 and m∠2 in the figure shown.


A. m∠1 = 60 and m∠2 = 120
B. m∠1 = 100 and m∠2 = 60
C. m∠1 = 120 and m∠2 = 60
D. m∠1 = 120 and m∠2 = 80

Solutions
Share 
Step: 1
If two parallel lines are cut by a transversal, then the pairs of Same-side interior angles are supplementary.
  [AB¯ and DC¯ are parallel lines cut by a transversal AD¯.]
Step: 2
∠1 + 120° = 180°
  [Same - side interior angles theorm.]
Step: 3
∠1 = 180° - 120° = 60°
  [Simplify.]
Step: 4
m∠1 + m∠2 = 180
  [Same - side interior angles theorm.]
Step: 5
60 + m∠2 = 180
  [From step 3.]
Step: 6
m∠2 = 180 - 60 = 120
  [Simplify.]
Step: 7
So, m∠1 = 60 and m∠2 = 120
Correct Answer is :   m∠1 = 60 and m∠2 = 120
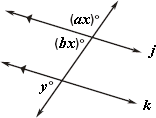
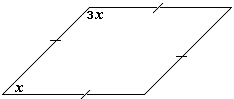
Q12The lines j and k are parallel. Find the values of x and y in the figure shown. [a = 10, b = 2.]


A. x = 15 and y = 17
B. x = 15 and y = 150
C. x = 15 and y = 30
D. x = 7 and y = 14

Solutions
Share 
Step: 1
10x° + 2x° = 180°
  [Adjacent angles.]
Step: 2
12x° = 180°
Step: 3
x° = 180°12 = 15°
Step: 4
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
  [Corresponding angles postulate .]
Step: 5
y = (2x)
  [From step 4.]
Step: 6
y = 2(15) = 30
Step: 7
So, x = 15 and y = 30
Correct Answer is :   x = 15 and y = 30
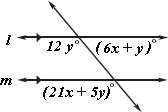
Q13The lines l and m are parallel. Find the values of x and y in the figure shown.


A. x = 6 and y = 18
B. x = 12 and y = 4
C. x = 4 and y = 8
D. x = 4 and y = 12

Solutions
Share 
Step: 1
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
  [Corresponding angles postulate.]
Step: 2
12y° = (21x + 5y)°
  [Corresponding angles.]
Step: 3
7y = 21x ⇒ y = 3x
  [Simplify.]
Step: 4
12y° + (6x + y)° = 180°
  [Adjacent angles.]
Step: 5
13y + (6x) = 180°
  [Simplify.]
Step: 6
13(3x) + 6x = 180 ⇒ 45x = 180
  [Substitute y = 3x and simplify.]
Step: 7
x = 18045 ⇒ x = 4
  [Simplify.]
Step: 8
y = 3(4) = 12
  [From step 3.]
Step: 9
So, the values of x and y are 4 and 12.
Correct Answer is :   x = 4 and y = 12
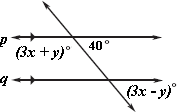
Q14The lines p and q are parallel. Find the values of x.

A. x = 40
B. x = 60
C. x = 50
D. x = 30

Solutions
Share 
Step: 1
From the data, one of the large angles is (3x + y)°.
Step: 2
From the data, two of the small angles are 40° and (3x - y)°.
Step: 3
If a transversal intersects two or more parallel lines, all small angles are equal.
Therefore, 3x - y = 40 ---- (1)
Step: 4
If a transversal intersects two or more parallel lines, then sum of small angle and large angle equals straight angle.
Therefore, 3x + y + 40 = 180
3x + y = 140 ---- (2)
Step: 5
Now, add equation (1) and equation (2) and solve for x.
6x = 180
x = 30
Correct Answer is :   x = 30
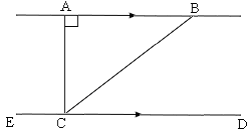
Q15From the given figure If ∠ECB = 150, then ∠ABC = _________ .

A. 30
B. 150
C. 330
D. 105

Solutions
Share 
Step: 1
m∠ECD = 180
  [∠ECD is a straight angle.]
Step: 2
m∠ECB + m∠BCD = 180
  [Angle Addition Postulate.]
Step: 3
150 + m∠BCD = 180
  [Substitute.]
Step: 4
m∠BCD = 30
  [Simplify.]
Step: 5
m∠ABC = m∠BCD
  [Alternate Interior Angles Theorem.]
Step: 6
m∠ABC = 30
  [Substitute.]
Correct Answer is :   30

HighSchool Math