Solved Examples and Worksheet for Properties of Isosceles Triangles

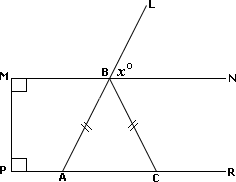
Q1In the figure, MN || PR, ∠LBN = x°, AB¯ = BC¯. Find m∠ABC if x = 63.


A. 52
B. 58
C. 63
D. 54

Solutions
Share 
Step: 1
m∠BAC = m∠LBN
  [Corresponding angles are congruent.]
Step: 2
m∠BAC = 63
  [Substitute m∠LBN = 63.]
Step: 3
In ΔABC, AB¯ = BC¯ ⇒ ∠BCA = ∠BAC
  [Isosceles triangle theorem.]
Step: 4
m∠BCA = 63
  [Step 2.]
Step: 5
m∠ABC = 180 - (m∠BAC + m∠BCA)
  [Triangle Angle-Sum theorem.]
Step: 6
m∠ABC = 180 - (63 + 63)
  [Substitute.]
Step: 7
m∠ABC = 54
  [Simplify.]
Correct Answer is :    54
Q2In the figure, PQ¯ = PR¯. m∠CPR = x. If x = 108, find m∠PQR.


A. 82
B. 108
C. 118
D. 72

Solutions
Share 
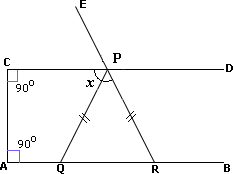
Step: 1
CD || AB
  [m∠DCA = m∠BAC = 90.]
Step: 2
m∠PRQ + m∠CPR = 180
  [Same side Interior angles theorem.]
Step: 3
m∠PRQ + 108 = 180
  [Substitute m∠CPR = 108.]
Step: 4
m∠PRQ = 72
  [Simplify.]
Step: 5
In ΔPQR, PQ¯ = PR¯ ⇒ ∠PQR = ∠PRQ
  [Isosceles triangle theorem.]
Step: 6
m∠PQR = 72
  [Substitute m∠PRQ = 72.]
Correct Answer is :    72
Q3In the figure, AB = BX and AC = CY. m∠ABC = a and m∠ACB = b. What is the measure of ∠XAY ? [Given a = 63 and b = 63.]

A. 113
B. 117
C. 121
D. 119

Solutions
Share 
Step: 1
In ΔXAB, ∠ABC = ∠BXA + ∠BAX
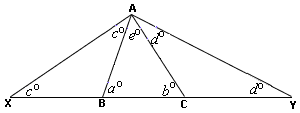
  [In a triangle, an exterior angle is equal to the sum of the opposite interior angles.]

Step: 2
In ΔXAB, AB = BX ⇒ ∠BXA = ∠BAX
  [Isosceles triangle theorem.]
Step: 3
m∠ABC = 2(m∠BAX)
  [Step 1 and Step 2.]
Step: 4
m∠BAX = 12(m∠ABC)
  [Rearrange.]
Step: 5
m∠BAX = 12(63)
  [Substitute.]
Step: 6
m∠BAX = 31.5
  [Simplify.]
Step: 7
Similarly, in ΔACY, m∠CAY = 12(m∠ACB)
Step: 8
m∠CAY = 12(63)
  [Substitute.]
Step: 9
m∠CAY = 31.5
  [Simplify.]
Step: 10
In ΔABC, m∠BAC = 180 - (m∠ABC + m∠ACB)
  [Triangle-Angle-Sum theorem.]
Step: 11
m∠BAC = 180 - (63 + 63)
  [Substitute.]
Step: 12
m∠BAC = 54
  [Simplify.]
Step: 13
m∠XAY = m∠XAB + m∠BAC + m∠CAY
  [Angle addition postulate.]
Step: 14
Here a = 63, b = 63, e = 54, c = 31.5 and d = 31.5.
Step: 15
m∠XAY = 31.5 + 54 + 31.5
  [Substitute.]
Step: 16
m∠XAY = 117
Correct Answer is :    117
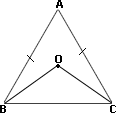
Q4OB¯ and OC¯ are the bisectors of ∠B and ∠C. If m∠A = 83, then find m∠BOC.


A. 131.50
B. 121.50
C. 129.50
D. 136.50

Solutions
Share 
Step: 1
In ΔABC, m∠A + m∠B + m∠C = 180
  [Triangle Angle-Sum theorem.]
Step: 2
In ΔABC, AB = AC ⇒ ∠B = ∠C
  [Isosceles triangle theorem.]
Step: 3
83 + m∠B + m∠B = 180
  [Step 1 and step 2.]
Step: 4
2(m∠B) = 97
  [Simplify.]
Step: 5
m∠B = 48.50
  [Solve for ∠B.]
Step: 6
m∠C = m∠B = 48.50
  [Step 2.]
Step: 7
m∠OBC = 12(m∠B) = 12(48.50) = 24.25
  [OB¯ is the bisector of ∠B.]
Step: 8
m∠OCB = 12(m∠C) = 12(48.50) = 24.25
  [OC¯ is the bisector of ∠C.]
Step: 9
In ΔBOC, m∠BOC = 180 - (m∠OBC + m∠OCB)
  [Triangle Angle sum theorem.]
Step: 10
m∠BOC = 180 - (24.25 + 24.25)
  [Substitute.]
Step: 11
m∠BOC = 131.50
  [Simplify.]
Correct Answer is :    131.50
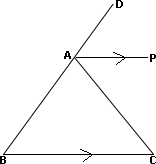
Q5In the figure, AP¯ is drawn parallel to BC¯. Also, AP¯ bisects ∠CAD. If m∠B = 57, then find m∠C.

A. 66
B. 57
C. 62
D. 61

Solutions
Share 
Step: 1
AP¯ || BC¯
  [Given.]
Step: 2
Let m∠DAP be x.
Step: 3
m∠B = m∠DAP
  [Corresponding angles postulate.]
Step: 4
m∠PAC = m∠DAP
  [AP¯ is bisector of ∠CAD.]
Step: 5
m∠PAC = x
  [Substitute m∠DAP = x.]
Step: 6
m∠ACB = m∠PAC
  [Alternate interior angles theorem.]
Step: 7
m∠C = m∠DAP
  [m∠ACB = m∠C and step 4.]
Step: 8
m∠B = m∠C
  [Step 3 and Step 7.]
Step: 9
m∠C = 57
  [m∠B = 57.]
Correct Answer is :    57
Q6ABC is a triangle. The bisector of the ∠BCA meets AB¯ at X. A point Y lies on CX¯ such that AX¯ = AY¯. If m∠CAY = 36, then find m∠ABC.
A. 45
B. 60
C. 90
D. 36

Solutions
Share 
Step: 1
Let m∠AXY be α and m∠XCB be θ.
Step: 2

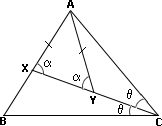
Step: 3
m∠XCA = m∠XCB = θ
  [CX¯ is bisector of ∠BCA.]
Step: 4
In ΔAXY, AX = AY ⇒ m∠AYX = m∠AXY
  [Isosceles triangle theorem.]
Step: 5
α = (m∠CAY) + (θ)
Step: 6
m∠CAY = (α - θ)
  [Rearrange.]
Step: 7
In ΔXBC, m∠AXC = m∠XBC + m∠XCB
  [Exterior angle theorem.]
Step: 8
α = (m∠XBC) + θ
  [Substitute.]
Step: 9
m∠XBC = (α - θ)
  [Rearrange.]
Step: 10
m∠XBC = m∠ABC
  [Same angle.]
Step: 11
m∠XBC = m∠CAY
  [Step 6 and step 11.]
Step: 12
m∠XBC = m∠CAY = m∠ABC = 36
  [Given that m∠CAY = 36.]
Correct Answer is :   36
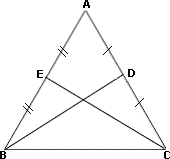
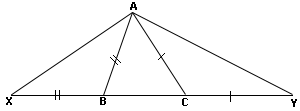
Q7In ΔABC, AB¯ = AC¯. If BD¯ and CE¯ are the medians of ΔABC and BD = 8 cm, then what is the length of CE?


A. 10 cm
B. 8 cm
C. 6 cm
D. 13 cm

Solutions
Share 
Step: 1
As AB¯ = AC¯ ⇒ ∠B = ∠C.
  [Isosceles Triangle.]
Step: 2
ΔEBC = ΔDCB
  [SAS property.]
Step: 3
CE = BD = 8 cm
  [ΔEBC ≅ ΔDCB.]
Correct Answer is :    8 cm
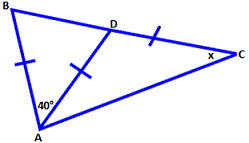
Q8In the figure, AB = AD = CD. Find the value of x in degrees.


A. 70°
B. 55°
C. 45°
D. 35°

Solutions
Share 
Step: 1
In ΔACD, AD = CD ⇒ m∠ACD = m∠CAD = x
  [Isosceles triangle theorem.]
Step: 2
In ΔADB, m∠ADB = m∠ACD + m∠CAD = x + x = 2x
  [Exterior angle theorem.]
Step: 3
In Δ ADB, AD = AB ⇒ m∠ABD = m∠ADB = 2x
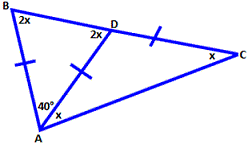
  [Isosceles triangle theorem.]

Step: 4
In ΔADB, m∠ABD + m∠ADB + m∠BAD = 180°
  [Triangle-Angle-Sum theorem.]
Step: 5
2x + 2x + 40° = 180°
Step: 6
4x = 180° - 40° = 140°
Step: 7
Therefore, x = 140°4 = 35°
Correct Answer is :   35°
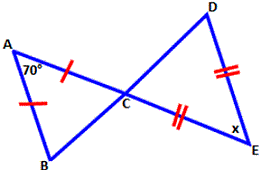
Q9In the figure shown, AB = AC and CE = DE. Find the value of x in degrees.


A. 65°
B. 55°
C. 70°
D. 60°

Solutions
Share 
Step: 1
Let m∠ABC be y.
Step: 2
In ΔABC, AB = AC ⇒ m∠ACB = m∠ABC = y
  [Isosceles triangle theorem.]
Step: 3
m∠DCE = m∠ACB = y
  [Vertically Opposite angles are equal.]
Step: 4
In ΔCDE, CE = DE ⇒ m∠CDE = m∠DCE = y
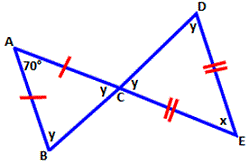
  [Isosceles triangle theorem.]

Step: 5
In ΔABC, m∠ABC + m∠ACB + m∠BAC = 180°
  [Triangle-Angle-Sum theorem.]
Step: 6
y + y + 70° = 180°
Step: 7
2y = 180° - 70° = 110°
Step: 8
So y = 110°2 = 55°
Step: 9
in ΔCDE, m∠DCE + m∠CDE + m∠CED = 180°
  [Triangle-Angle-Sum theorem.]
Step: 10
y + y + x = 180°
Step: 11
x = 180° - 2y = 180° - 2 × 55°
Step: 12
Therefore, x = 180° - 110° = 70°
Correct Answer is :   70°
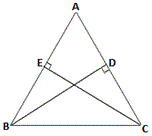
Q10In ΔABC, BD¯ and CE¯ are altitudes and BD = CE. Then which of the following statements is incorrect ?


A. ΔABC may be an equilateral triangle
B. ΔABC may be an isoceles triangle
C. ΔABC is a scalene triangle
D. ΔABC is an isoceles or an equilateral triangle

Solutions
Share 
Step: 1

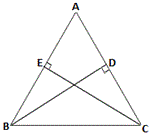
Step: 2
Area of ΔABC = 12 × AC × BD = 12 × AB × CE
  [Area of triangle = 12× base × altitude.]
Step: 3
So, AB = AC
  [BD = CE.]
Step: 4
Therefore, ΔABC is an isosceles or an equilateral triangle
  [From Step 3]
Correct Answer is :   ΔABC is a scalene triangle

HighSchool Math