Solved Examples and Worksheet for Angle Sum Theorem and Medians in a Triangle

Q1What are the angles of a triangle which are in the ratio 4 : 5 : 6?
A. 58o, 81o, 77o
B. 38o, 55o, 72o
C. 48o, 60o, 72o
D. 96o, 60o, 97o

Solutions
Share 
Step: 1
Let 4x, 5x and 6x be the angles.
Step: 2
4x + 5x + 6x = 180o
  [Triangle angle sum theorem.]
Step: 3
15x = 180o
x = 180°15
x = 12o
  [Divide each side by 15.]
Step: 4
So, 4x = 4 × 12o = 48o
5x = 5 × 12o = 60o
6x = 6 × 12o = 72o
  [Substitute x = 12o.]
Step: 5
The angles of the triangle are 48o, 60o and 72o .
Correct Answer is :   48o, 60o, 72o
Q2If m∠A + m∠B = 90, then what all can be concluded from this?
(i) One arm of ∠A and one arm of ∠B are perpendicular
(ii). ∠A and ∠B are complementary.
(iii). m∠A = 90 - m∠B
(iv) m∠B = 90 - m∠A
(v). ∠A and ∠B cannot be the angles of the same triangle.

A. (i), (ii) and (v)
B. (ii), (iii), (iv) and (v)
C. All statements
D. (ii), (iii) and (iv)

Solutions
Share 
Step: 1
The two angles can be with two different arms. Statement (i) need not be correct.
Step: 2
The two angles can be the angles of the same triangle since sum of the angles of a triangle is 180 degrees.
Step: 3
(ii), (iii) and (iv) are correct.
Correct Answer is :   (ii), (iii) and (iv)
Q3Find the value of 2y + 3z.

A. 200
B. 300
C. 350
D. 250

Solutions
Share 
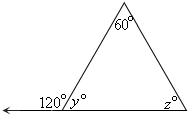
Step: 1
y + 120 = 180
  [Linear pair.]
Step: 2
y = 180 - 120 = 60
  [Simplify.]
Step: 3
The sum of the measures of the angles of a triangle is 180.
  [Triangle angle sum theorem.]
Step: 4
60 + y + z = 180
  [From step 3.]
Step: 5
60 + 60 + z = 180
  [Substitute 60 for y.]
Step: 6
z = 180 - 120 = 60
  [Simplify.]
Step: 7
So, 2y + 3z = 120 + 180 = 300
  [Substitute 60 for y and z.]
Correct Answer is :   300
Q4Find the values of x and y.


A. 72 and 36
B. 36 and 72
C. 36 and 36
D. 72 and 72

Solutions
Share 
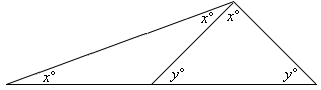
Step: 1
The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles.
  [Exterior angle theorem.]
Step: 2
y = 2x
  [From step 1.]
Step: 3
The sum of the measure of the angles of a triangle is 180.
  [Triangle angle-sum theorem.]
Step: 4
x + y + y = 180
  [From step 3.]
Step: 5
x + 2x + 2x = 180
  [Substitute y = 2x.]
Step: 6
5x = 180 ⇒ x = 36
  [Simplify.]
Step: 7
y = 2x ⇒ 2(36) = 72
  [From step 2.]
Step: 8
Hence the value of x is 36 and y is 72.
Correct Answer is :   36 and 72
Q5If the angles of a triangle are in the ratio of 2 : 4 : 6, find the largest angle.

A. 90°
B. 120°
C. 60°
D. 100°

Solutions
Share 
Step: 1
Since the measures of the angles of the triangle are in the ratio 2: 4: 6, the measures of the angles of triangle can be taken as 2x, 4x and 6x.
Step: 2
The sum of the measure of angles of a triangle is 180.
  [Triangle angle sum theorem.]
Step: 3
2x + 4x + 6x =180
  [ From steps 1 and 2 ]
Step: 4
12x= 180
  [Simplify]
Step: 5
x = 15
  [solve for x]
Step: 6
The measures of the angles of triangle are,
Step: 7
2x = 2(15) = 30,
Step: 8
4x=4(15) = 60 and
Step: 9
6x = 6(15) = 90
Step: 10
Therefore, the largest angle of a triangle = 90°.
Correct Answer is :   90°
Q6The measures of angles of a triangle are perfect squares. Find the difference between the largest and the smallest angles.
A. 84°
B. 6°
C. 36°
D. 48°

Solutions
Share 
Step: 1
The sum of all the three angles in a triangle is 180°.
  [Angle sum theorem of a triangle.]
Step: 2
The measures of angles of a triangle are perfect squares.
  [Given.]
Step: 3
If the angles of a triangle are a°, b°, and c°, then a + b + c = 180°, where a, b, and c are perfect squares.
Step: 4
Let the angles be a = 16°, b = 64°, and c = 100°.
Step: 5
⇒ 16 + 64 + 100 = 180
  [16 = 42, 64 = 82, and 100 = 102.]
Step: 6
Here, the largest angle is 100 and the smallest angle is 16.
Step: 7
So, the difference between the largest and the smallest angles = 100 - 16 = 84°.
Correct Answer is :   84°
Q7If x = 62°, then find the missing angle shown in the figure.


A. 28°
B. 45°
C. 36°
D. cannot be determined

Solutions
Share 
Step: 1
The sum of all the angle measures of a triangle is 180°.
Step: 2
90° + 62° + y° = 180°
  [Equate the sum of angles of the triangle to 180°.]
Step: 3
152° + y° = 180°
  [Add.]
Step: 4
y° = 28°
  [Subtract 152° from each side.]
Correct Answer is :   28°
Q8What are the measures of the angles of a triangle, if they are in the ratio 5 : 6 : 7 ?

A. 100°, 60°, 95°
B. 40°, 55°, 70°
C. 60°, 81°, 75°
D. 50°, 60°, 70°

Solutions
Share 
Step: 1
Let 5x, 6x and 7x be the angles.
Step: 2
Sum of the measures of the angles in a triangle = 180°
Step: 3
5x + 6x + 7x = 180°
18x = 180°
x = 180°18
x = 10°
  [Divide each side by 18.]
Step: 4
5x = 5 × 10° = 50°
6x = 6 × 10° = 60°
7x = 7 × 10° = 70°
  [Substitute x = 10° .]
Step: 5
The measures of the angles are 50°, 60° and 70° .
Correct Answer is :   50°, 60°, 70°
Q9Which of the following is incorrect?
A. The three medians of a triangle are always concurrent inside of it.
B. A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side.
C. The point of concurrency of the three medians of a triangle is called the centroid.
D. The length of the median from the centroid to the opposite side of the vertex is equal to the length of the median from the vertex to the centroid.

Solutions
Share 
Step: 1
The centroid of a triangle divides the medians in the ratio 2:1. That is AG : GD = 2 : 1
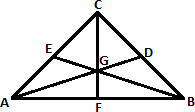
Step: 2
AGGD = 21⇒ GD = 12 AG
Step: 3
Therefore, the length of the median from the centroid to the opposite side of the vertex is equal to half the length of the median from the vertex to the centroid.
Correct Answer is :   The length of the median from the centroid to the opposite side of the vertex is equal to the length of the median from the vertex to the centroid.
Q10In ΔABC, AD is the median and G is the centroid. Find the ratio of AD : GD?
A. 3 : 1
B. 2 : 1
C. 3 : 2
D. 1 : 2

Solutions
Share 
Step: 1

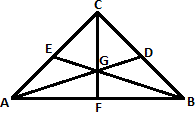
Step: 2
The centroid of a triangle divides the medians in the ratio 2:1.
Step: 3
That is AG : GD = 2 : 1.
Step: 4
AGGD = 21 ⇒ AG = 2GD.
Step: 5
AD = AG + GD = 2 GD + GD = 3 GD.
Step: 6
⇒ ADGD = 31
Step: 7
Therefore,AD : GD = 3 : 1.
Correct Answer is :   3 : 1
Q11Which of the following is correct?

A. No median coincides with an altitude in an isosceles triangle.
B. At least one median coincides with an altitude in both isosceles and equilateral triangles.
C. No median coincides with an altitude in an equilateral triangle.
D. No median coincides with an altitude either in an isosceles triangle or in an equilateral triangle.

Solutions
Share 
Step: 1
In an equilateral triangle, the median from any vertex to the opposite side will be perpendicular to that side.
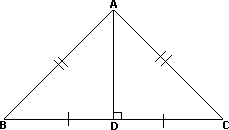
Step: 2
In an isosceles triangle, the median from the vertex containing the congruent sides is perpendicular to the base.
Step: 3
So, in both isosceles triangle and equilateral triangle, at least one median coincides with an altitude.
Correct Answer is :   At least one median coincides with an altitude in both isosceles and equilateral triangles.
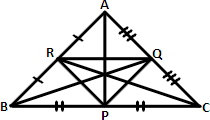
Q12AP, BQ and CR are the medians of ΔABC.If the lengths of PQ = 8 cm, QR = 10 cm and PR =12 cm , then the lengths of AB, BC and AC are ______.

A. 16 cm, 20 cm and 24 cm respectively
B. 4 cm, 5 cm and 6 cm respectively
C. 12 cm, 15 cm and 18 cm respectively
D. 8 cm, 10 cm and 12 cm respectively

Solutions
Share 
Step: 1
PQ || AB, QR || BC, PR ||AC
  [Mid-segment theorem.]
Step: 2
PQ = 12 AB ⇒ AB = 2 PQ = 2 × 8 = 16 cm.
Step: 3
QR = 12 BC ⇒ BC = 2 QR = 2 × 10 = 20 cm.
Step: 4
PR = 12 AC ⇒ AC = 2 PR = 2 × 12 = 24 cm.
Correct Answer is :   16 cm, 20 cm and 24 cm respectively
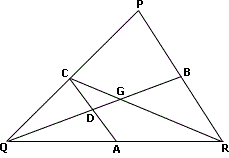
Q13A, B and C are the mid points of the three sides of ΔPQR as shown in the figure. QB and CR intersect at G. If BD = 15 cm, find the length of GD.

A. 5 cm
B. 8 cm
C. 10 cm
D. 15 cm

Solutions
Share 
Step: 1
ΔPQR ~ ΔCQA
  [A and C are midpoints of QR and PQ and AC is the midsegment.]
Step: 2
⇒ QDQB = 12⇒ QDQD + DB = 12
  [Ratio of the sides of the similar triangles ΔCQA and ΔPQR is 1 : 2.]
Step: 3
2QD = QD + DB ⇒ QD = DB = 15 cm
  [DB = BD = 15 cm.]
Step: 4
QB = QD + DB = 15 cm + 15 cm = 30 cm
Step: 5
QG = 23 × QB = 23 × 30 = 20 cm
  [G is the point of intersection of the medians, which divides the median in 2 : 1 ratio.]
Step: 6
GD = QG - QD = 20 - 15 = 5 cm
Correct Answer is :   5 cm

HighSchool Math