ALTERNATE INTERIOR ANGLES
Definition Of Alternate Interior Angles
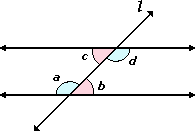
When two lines are cut by a transversal, the pair of angles formed interior of the two lines and on the opposite of the transversal is called Alternate Interior Angles.
More About Alternate Interior Angles:
If two parallel lines are cut by a transversal, the alternate interior angles are congruent
Examples of Alternate Interior Angles
In the figure shown, l is the transversal that cut the pair of lines. Angles a and d and angles b and c are alternate interior angles.
Video Examples: Alternate Interior Angles
Solved Example on Alternate Interior Angles
Ques: Find the measure of angle m in the figure shown.
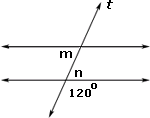
Choices:
A. 120o
B. 180o
C. 60o
D. Insufficient information
Correct Answer: C
Solution:
Step 1: 120o + n = 180o [Straight angle.]
Step 2: n = 60o [Solve for n.]
Step 3: n = 60o implies m = 60o, because m and n are alternate interior angles and so they are congruent.
Quick Summary
- Alternate interior angles are formed when a transversal intersects two lines.
- If the two lines are parallel, the alternate interior angles are congruent.
🍎 Teacher Insights
Use visual aids and hands-on activities to help students identify alternate interior angles. Emphasize the importance of parallel lines for the congruence of these angles.🎓 Prerequisites
- Parallel Lines
- Transversals
- Angles
Check Your Knowledge
Q1: Which angles are alternate interior angles?
Q2: If two parallel lines are cut by a transversal and one angle is 60 degrees, what is the measure of its alternate interior angle?
Frequently Asked Questions
Q: Are alternate interior angles always congruent?
A: No, alternate interior angles are only congruent when the two lines cut by the transversal are parallel.
Q: What is a transversal?
A: A transversal is a line that intersects two or more other lines.