Solved Examples and Worksheet for Graphing and Analyzing Quadratic Functions

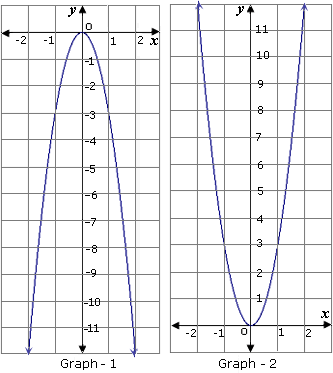
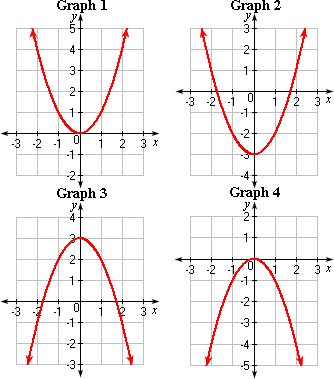
Q1Graph the quadratic function y = 3x2. Indicate whether the parabola opens upward or downward. Determine the equation of the axis of symmetry and the coordinates of the vertex. Also mention if the vertex is a maximum or a minimum point.

A. Graph 2; opens up; x = 0; (0, 0); Minimum point
B. Graph 1; opens up; x = 0; (0, 1); Minimum point

Solutions
Share 
Step: 1
Make a table of ordered pairs for the given function.
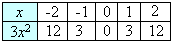
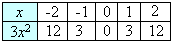
Step: 2
Plot these points on the coordinate plane and connect the points with a smooth curve.
Step: 3
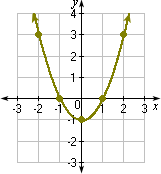
The graph looks like the one below:
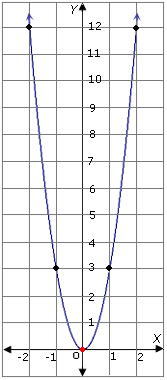
Step: 4
It can be observed from the graph that the parabola opens upward.
Step: 5
The equation of the axis of symmetry is: x = 0.
Step: 6
The vertex is at (0, 0).
Step: 7
The parabola opens up. So the vertex is the minimum point.
Correct Answer is :   Graph 2; opens up; x = 0; (0, 0); Minimum point
Q2Which graph best represents the quadratic function y = - x2 + 1?


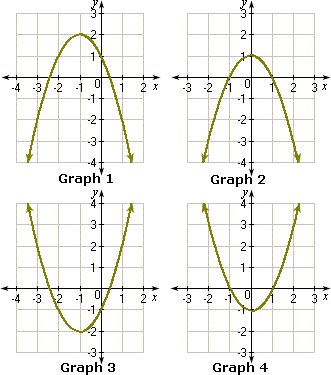
A. Graph 2
B. Graph 1
C. Graph 3
D. Graph 4

Solutions
Share 
Step: 1
y = - x2 + 1
  [Original quadratic function.]
Step: 2
a = - 1, b = 0, and c = 1
  [Comparing with y = ax2 + bx + c.]
Step: 3
The x-coordinate of the vertex = - b2a = - 02(- 1) = 0
Step: 4
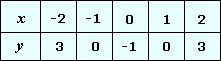
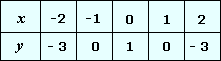
The values of y = - x2 + 1 for the x-values to the left and right of x = 0 are tabulated below:
Step: 5
Plot the points and join them with a smooth curve as shown.
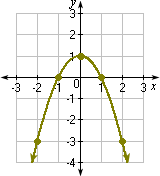
Step: 6
The graph matches with Graph 2.
Correct Answer is :   Graph 2
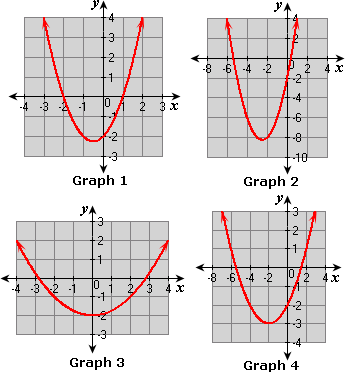
Q3Which of the graphs best suits the quadratic function?
y = x24 - 2

A. Graph 1
B. Graph 2
C. Graph 3
D. Graph 4

Solutions
Share 
Step: 1
y = x24 - 2
  [Original quadratic function.]
Step: 2
a = 14, b = 0 and c = - 2
  [Comparing with y = ax2 + bx + c.]
Step: 3
The x-coordinate of the vertex = - b2a = - 02(14) = 0
Step: 4
The values of y = (x24) - 2 for the x-values to the left and right of x = 0 are:
Step: 5
Graph 3 satisfies the above table.
Correct Answer is :   Graph 3
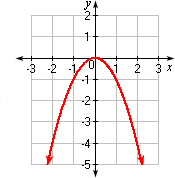
Q4Which is the graph of the quadratic function y = - x2?

A. Graph 2
B. Graph 1
C. Graph 3
D. Graph 4

Solutions
Share 
Step: 1
y = - x2
  [Original function.]
Step: 2
a = - 1, b = 0, and c = 0
  [Comparing with y = ax2 + bx + c.]
Step: 3
The x-coordinate of the vertex = - b2a = - 02(- 1) = 0
Step: 4
The values of y = - x2 for the x-values to the left and right of x = 0 are tabulated below:
Step: 5
Plot the points and join them with a smooth curve as shown.
Step: 6
The graph matches with Graph 4.
Correct Answer is :   Graph 4
Q5Which graph best represents the quadratic function y = x2 - 1?

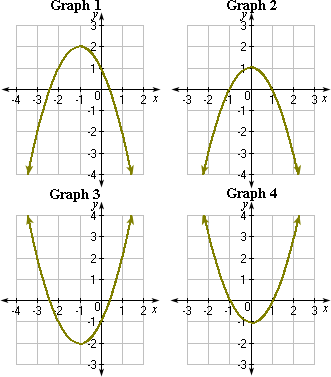
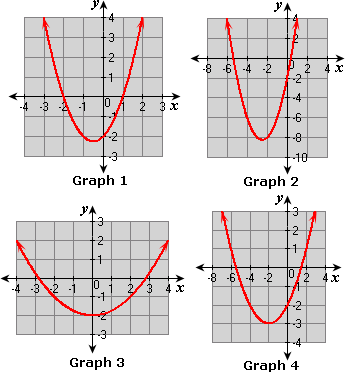
A. Graph 2
B. Graph 1
C. Graph 3
D. Graph 4

Solutions
Share 
Step: 1
y = x2 - 1
  [Original quadratic function.]
Step: 2
a = 1, b = 0, and c = - 1
  [Comparing with y = ax2 + bx + c.]
Step: 3
The x-coordinate of the vertex = - b2a = - 02(1) = 0
Step: 4
The values of y = x2 - 1 for the x-values to the left and right of x = - 1 are tabulated below:
Step: 5
Plot the points and join them with a smooth curve as shown.
Step: 6
The graph matches with Graph 4.
Correct Answer is :   Graph 4
Q6Which of the graphs best suits the quadratic function?
y = x2 + 5x - 2


A. Graph 1
B. Graph 3
C. Graph 2
D. Graph 4

Solutions
Share 
Step: 1
y = x2 + 5x - 2
  [Original quadratic function.]
Step: 2
a = 1, b = 5 and c = - 2
  [Comparing with y = ax2 + bx + c.]
Step: 3
The x-coordinate of the vertex = - b2a = - 52(1) = - 2.5
Step: 4
The values of y = x2 + 5x - 2 for the x-values to the left and right of x = - 2.5 are:
Step: 5
Graph 2 satisfies the above table.
Correct Answer is :   Graph 2

HighSchool Math