Solved Examples and Worksheet for Finding Intercepts of Quadratic Functions

Q1Find the number of x-intercepts of the graph y = -7x2 + 3x - 7.

A. Two
B. Zero
C. One
D. Many

Solutions
Share 
Step: 1
y = -7x2 + 3x - 7
  [Original equation.]
Step: 2
The x-intercepts occur when y = 0.
Step: 3
0 = -7x2 + 3x - 7
  [Substitute 0 for y.]
Step: 4
Compare the equation with the standard form to get the values of a, b and c.
Step: 5
b2 - 4ac = (3)2 - 4(-7)(-7)
  [Substitute a = -7, b = 3 and c = -7 in the discriminant.]
Step: 6
= -187
  [Simplify.]
Step: 7
Since the discriminant is negative, the quadratic equation has no real solution.
Step: 8
So, the graph has no x-intercepts.
Correct Answer is :   Zero
Q2Find the x-intercepts by graphing the related function of the equation - x2 - 4x = 3.

A. 3 and - 1
B. - 3 and 1
C. 3 and 1
D. - 3 and - 1

Solutions
Share 
Step: 1
ax2 + bx + c = 0
  [Standard form of a quadratic equation.]
Step: 2
- x2 - 4x = 3
  [Original equation.]
Step: 3
- x2 - 4x - 3 = 0
  [Subtract 3 from each side.]
Step: 4
Sketch the graph of the related quadratic function y = - x2 - 4x - 3 as shown below:
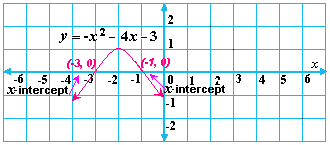
Step: 5
In the graph shown, the x-intercepts are - 3 and - 1.
Correct Answer is :   - 3 and - 1
Q3Find the number of x-intercepts of the graph y = - 3x2 + 2x - 3.

A. Two
B. One
C. Many
D. Zero

Solutions
Share 
Step: 1
y = - 3x2 + 2x - 3
  [Original equation.]
Step: 2
The x-intercepts occur when y = 0.
Step: 3
0 = - 3x2 + 2x - 3
  [Replace y with 0.]
Step: 4
Compare the equation with the standard form to get the values of a, b and c.
Step: 5
b2 - 4ac = (2)2 - 4(- 3)(- 3)
  [Substitute a = - 3, b = 2 and c = - 3 in the discriminant.]
Step: 6
= -32
  [Simplify.]
Step: 7
Since the discriminant is negative, the quadratic equation has no real solution.
Step: 8
So, the graph has no x-intercepts.
Correct Answer is :   Zero
Q4Find the number of x-intercepts of the graph y = - 6x2 + 5x - 6.

A. One
B. Many
C. Zero
D. Two

Solutions
Share 
Step: 1
y = - 6x2 + 5x - 6
  [Original equation.]
Step: 2
The x-intercepts occur when y = 0.
Step: 3
0 = - 6x2 + 5x - 6
  [Replace y with 0.]
Step: 4
Compare the equation with the standard form to get the values of a, b and c.
Step: 5
b2 - 4ac = (5)2 - 4(- 6)(- 6)
  [Substitute a = - 6, b = 5 and c = - 6 in the discriminant.]
Step: 6
= -119
  [Simplify.]
Step: 7
Since the discriminant is negative, the quadratic equation has no real solution.
Step: 8
So, the graph has no x-intercepts.
Correct Answer is :   Zero
Q5Find the number of x-intercepts of the graph y = x2 + 4x + 4.
A. Zero
B. Many
C. Two
D. One

Solutions
Share 
Step: 1
y = x2 + 4x + 4
  [Original equation.]
Step: 2
The x-intercepts occur when y = 0.
Step: 3
0 = x2 + 4x + 4
  [Replace y with 0.]
Step: 4
Compare the equation with the standard form to get the values of a, b and c.
Step: 5
b2 - 4ac = (4)2 - 4(1)(4)
  [Substitute a = 1, b = 4 and c = 4 in the discriminant.]
Step: 6
= 16 - 16 = 0
  [Simplify.]
Step: 7
Since the discriminant is equal to zero, the quadratic equation has only one solution.
Step: 8
So, the graph has one x-intercept.
Correct Answer is :   One

HighSchool Math