Solved Examples and Worksheet for Graphing Trigonometric Functions
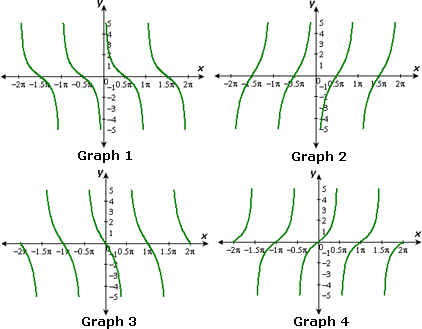
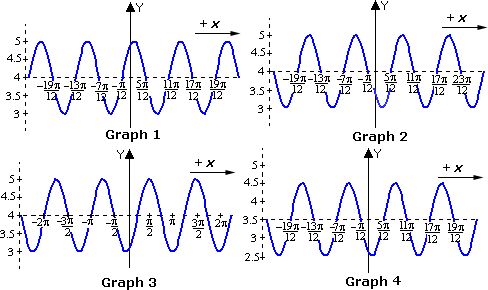
A. Graph 3
B. Graph 1
C. Graph 2
D. Graph 4
Step: 1
Make a table of values for ordered pairs of the form (x x
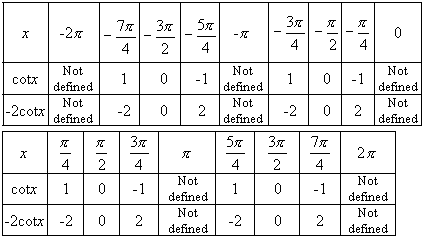

Step: 2
Plot the points and connect them with a smooth curve. Draw dashed vertical lines at the points where the function y x
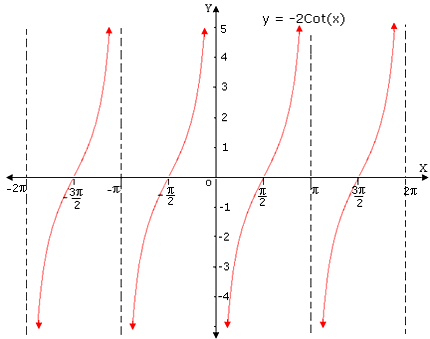

Step: 3
The dashed vertical lines are the asymptotes. That is the graph of y x
Step: 4
Notice that the - 2 cot x π y x π
Correct Answer is : Graph 2
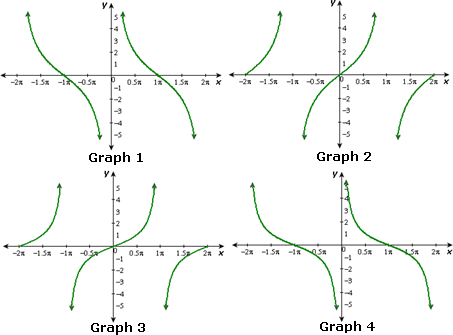
A. Graph 2
B. Graph 3
C. Graph 1
D. Graph 4
Step: 1
Make a table of values for ordered pairs of the form (x x 2
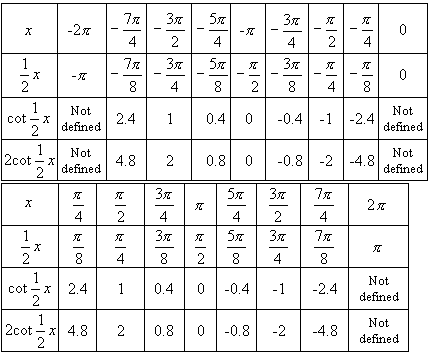

Step: 2
Plot the points and connect them with a smooth curve. Draw dashed vertical lines at the points where the function y x 2
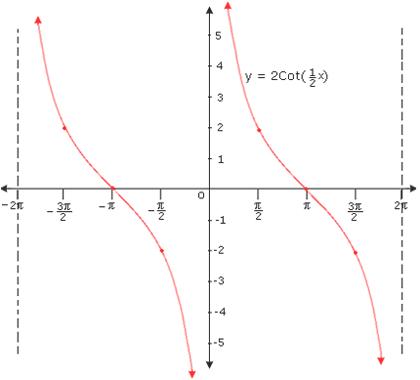

Step: 3
Notice that the function repeats at intervals of 2π y x 2 π
Correct Answer is : Graph 1
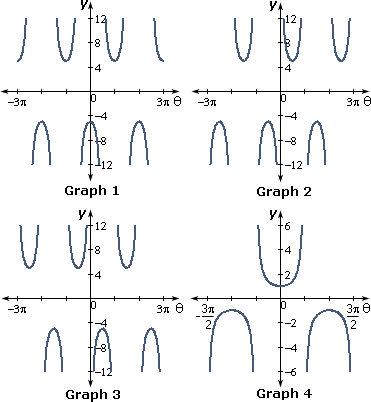
A. Graph 2
B. Graph 1
C. Graph 4
D. Graph 3
Step: 1
The graph of y a b θ a a
Step: 2
From the given function, we can identify the values of a b
Step: 3
Set b θ b θ π
Step: 4
We obtain θ θ π
[b
Step: 5
Make a table for θ π
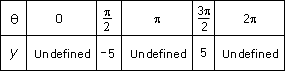

Step: 6
The above table matches with graph 3.
Step: 7
So, the graph of y θ
Correct Answer is : Graph 3
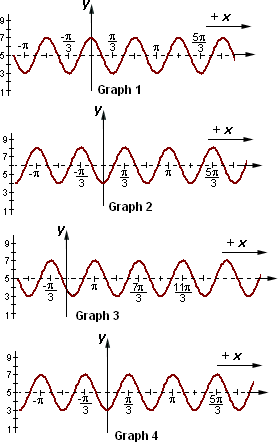
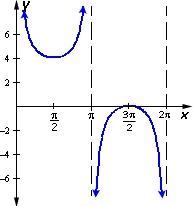
A. Graph 4
B. Graph 3
C. Graph 2
D. Graph 1
Step: 1
[Original function.]
Step: 2
It is clear that the centerline is 5 and amplitude is 2, this eliminates Graph 2.
[Since the centerline of Graph 2 is 6.]
Step: 3
From the argument (x π 3 π 3
Step: 4
The phase angle of the cosine function 2 cos 3(x π 3
Step: 5
The curve reaches the highest point at every half period. The period of this function is 2 π 3 π 3
Step: 6
As the half period of the function is - π 3 π 3
Step: 7
Indicate the location of the y π 3 π 3
Step: 8
Among the given graphs, Graph 4 represents the function y x π 3 )

Correct Answer is : Graph 4
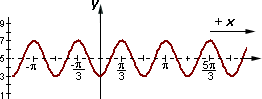
A. Graph 3
B. Graph 4
C. Graph 1
D. Graph 2
Step: 1
[Original function.]
Step: 2
It is clear that centerline is 5 and amplitude is 1. This eliminates Graph 2 and Graph 4.
[Centerline of Graph 2 is 4, and amplitude of Graph 4 is 2.]
Step: 3
From the argument (x π 2 π 2
[Phase angle of Graph 1 is taken as - π 2
Step: 4
The curve will cross its centerline at every half period. The period for this function is π 2 π 4 π 4 π 2
Step: 5
Indicate the location of y π 2 π 2
Step: 6
Among the given graphs, Graph 3 represents the function y x π 2
Correct Answer is : Graph 3
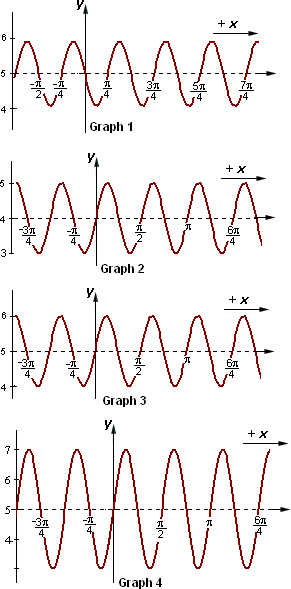
A. Graph 3
B. Graph 1
C. Graph 2
D. Graph 4
Step: 1
[Original function.]
Step: 2
It is clear that the centerline is + 5 and the amplitude is 1. This eliminates Graph 1.
[Since the center line of Graph 1 is + 6.]
Step: 3
Since the given function has negative sine function, so we can eliminate Graph 3.
Step: 4
From the argument (x π 2 ) π 2
Step: 5
The curve will cross its centerline every half period. The period for this function is π. Half period is π 2 π 2 π 2
Step: 6
Since 0° will lie between - π 2 π 2 y π 2 π 2
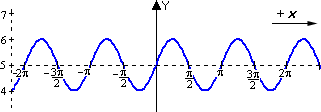

Step: 7
Thus Graph 4 represents the function y x π 2 )
Correct Answer is : Graph 4
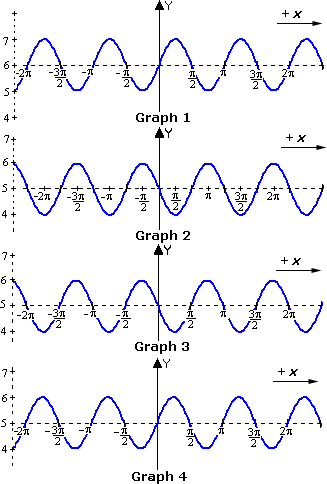
A. Graph 1
B. Graph 4
C. Graph 2
D. Graph 3
Step: 1
[Original function.]
Step: 2
It is clear that the centerline is + 4 and the amplitude is 1. This eliminates Graph 4.
[Since the center line of Graph 4 is + 3.5.]
Step: 3
Since the given function has positive sine function, so we can eliminate Graph 1.
Step: 4
From the argument (x 5 π 1 2 5 π 1 2
Step: 5
The curve will cross its centerline every half period. The period for this function is π. Half period is π 2 π 2 5 π 1 2
Step: 6
Since 0° will lie between - π 1 2 5 π 1 2 y π 1 2 5 π 1 2
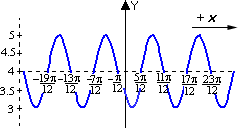

Step: 7
Thus Graph 2 represents the function y x 5 π 1 2 )
Correct Answer is : Graph 2
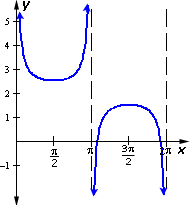
A.
B.
C.
D.
Step: 1
To get the equation of the graph first draw and identify the sinusoidal.
Step: 2
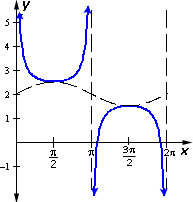
Step: 3
The centerline is at 2. The sinusoidal is y x
Step: 4
So the graph is y x
Correct Answer is : y x
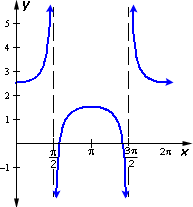
A.
B.
C.
D.
Step: 1
To get the equation of the graph first draw and identify the sinusoidal.
Step: 2
Step: 3
The centerline is at 2. The sinusoidal is y x
Step: 4
So the graph is y x
Correct Answer is : y x
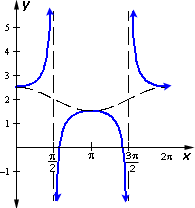
A.
B.
C.
D.
Step: 1
To get the equation of the graph first draw and identify the sinusoidal.
Step: 2
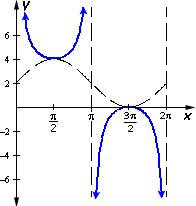
Step: 3
The centerline is at 2. The sinusoidal is y x
Step: 4
So the graph is y x
Correct Answer is : y x
- Determining a given Relation is a Function-Algebra1-Solved Examples
- Finding Values of a Function for a given Domain-Algebra1-Solved Examples
- Graphing Linear Functions for a Given Domain-Algebra1-Solved Examples
- Graphing Linear Functions-Algebra1-Solved Examples
- Finding the Rate of Change-Algebra1-Solved Examples
- Finding Intercepts of a Linear Equation-Algebra1-Solved Examples
- Graphing Piecewise and Step Functions-Algebra1-Solved Examples
- Graphing Absolute Value Functions-Algebra1-Solved Examples
- Finding Intercepts of Quadratic Functions-Algebra1-Solved Examples
- Graphing and Analyzing Quadratic Functions-Algebra1-Solved Examples
- Identifying and Graphing Square Root Functions-Algebra1-Solved Examples
- Comparing Properties of Two Functions-Algebra1-Solved Examples
- Finding Intervals for Increasing and Decreasing Functions-Algebra1-Solved Examples
- Representing Exponential Functions Using Tables or Graphs-Algebra1-Solved Examples
- Graphing Logarithmic Functions-Algebra1-Solved Examples
- Identifying and Using Recursive Formula-Algebra1-Solved Examples
Related Worksheet
- Surface Area