Solved Examples and Worksheet for Similar Figures

Q1D is a point on side BC of ΔABC such that m∠ADC = m∠BAC. If CA = 18 cm and CB = 24 cm, then what is the length of CD¯?

A. 13.5 cm
B. 32 cm
C. 12 cm
D. 9 cm

Solutions
Share 
Step: 1

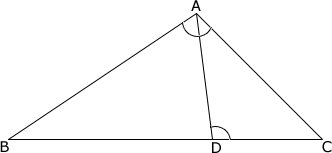
Step: 2
m∠ADC = m∠BAC
  [Given.]
Step: 3
m∠ACD = m∠ACB
Step: 4
ΔABC ~ ΔDAC
  [AA similarity postulate.]
Step: 5
CACD = CBCA
  [ΔABC is similar to ΔDAC.]
Step: 6
18CD = 2418
  [Substitute.]
Step: 7
CD = 32424
  [Cross product property.]
Step: 8
CD = 13.5 cm
  [Simplify.]
Correct Answer is :    13.5 cm
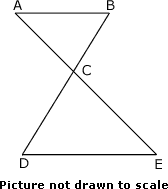
Q2In the figure, AB¯ || DE¯. AC = 4 cm, CE = 6 cm and DB = 5 cm. Find BC¯.

A. 4 cm
B. 3 cm
C. 3 cm
D. 2 cm

Solutions
Share 
Step: 1
Let BC = x cm
Step: 2
DC = DB - BC = (5 - x) cm
Step: 3
∠ACB ≅ ∠ECD
  [Vertically opposite angles are congruent.]
Step: 4
∠BAC ≅ ∠DEC
  [Alternate angles are congruent]
Step: 5
ΔACB ~ ΔECD
  [AA similarity postulate.]
Step: 6
ACEC = BCDC
  [Corresponding sides of similar triangles are proportional]
Step: 7
46 = x5-x
Step: 8
6x = 4(5 - x)
  [Cross multiply.]
Step: 9
6x = 20 - 4x
  [Multiply.]
Step: 10
10x = 20
  [Combine like terms.]
Step: 11
x = 2010
  [Divide by 10 on both sides.]
Step: 12
x = 2
  [Simplify.]
Step: 13
BC = 2 cm
Correct Answer is :   2 cm
Q3ΔPQR is similar to ΔABC. If PQ = 3 in., PR = 5 in., and AB = 8 in., then find AC.
A. 12 in.
B. 1313 in.
C. 178 in.
D. 10 in.

Solutions
Share 
Step: 1
ΔPQR and ΔABC are similar so that the corresponding sides are proportional. Thus, we can write proportions to find the measure of AC¯.
Step: 2
PQAB = PRAC
  [Write a proportion.]
Step: 3
38 = 5AC
  [Substitute the values.]
Step: 4
3AC = 40
  [Cross products.]
Step: 5
AC = 1313
  [Solve.]
Correct Answer is :   1313 in.
Q4Polygon ABCD is similar to polygon EFGH. Find the value of n, if a = 12 units, b = 30 units and c = 20 units.


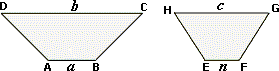
A. 50 units
B. 10 units
C. 8 units
D. 11 units

Solutions
Share 
Step: 1
If two polygons are similar, then the corresponding sides are in proportion.
Step: 2
CDGH = ABEF
  [CD corresponds to GH and AB corresponds to EF.]
Step: 3
3020 = 12n
  [Substitute the values.]
Step: 4
30 × n = 12 × 20
  [Write the cross products.]
Step: 5
30n = 240
  [Multiply.]
Step: 6
n = 8
  [Divide both sides by 30.]
Step: 7
The value of n is 8 units.
Correct Answer is :   8 units
Q5Choose the incorrect statement/s.
I. The corresponding angles of similar polygons are always congruent.
II. Two similar polygons are always congruent.
III. The corresponding sides of similar polygons are always congruent.
A. I and II only
B. II only
C. II and III only
D. III only

Solutions
Share 
Step: 1
The corresponding angles of similar polygons are congruent.
  [By definition.]
Step: 2
Two congruent figures are always similar but two similar polygons need not be congruent.
  [By definition.]
Step: 3
The corresponding sides of similar polygons are proportional but need not be congruent.
  [By definition.]
Step: 4
So, statements II and III are incorrect.
Correct Answer is :   II and III only
Q6Which of the following statement/s are not true about similarity?
I. All parallelograms are not similar.
II. All equilateral triangles are similar.
III. All isosceles triangles are similar.
IV. All congruent triangles are similar.
A. I only
B. II and IV only
C. III and IV only
D. III only

Solutions
Share 
Step: 1
Amongst the choices, the statement "all isosceles triangles are similar" is the incorrect statement.
Correct Answer is :   III only
Q7Which of the following is/are not true for two similar triangles?
I. Corresponding angles are congruent.
II. Corresponding sides are proportional.
III. Corresponding sides are congruent.
A. I and II only
B. II and III only
C. III only
D. I only

Solutions
Share 
Step: 1
The corresponding angles of similar polygons are congruent.
  [By definition.]
Step: 2
For similar triangles, corresponding sides are proportional but need not be congruent.
  [By definition.]
Step: 3
So, statement III is incorrect.
Correct Answer is :   III only
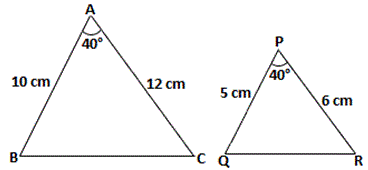
Q8Which theorem can prove ΔABC and ΔPQR similar?

A. SSS similarity theorem
B. AA similarity
C. SSA similarity theorem
D. SAS similarity theorem

Solutions
Share 
Step: 1
From the figure, we have ∠ A ≅ ∠P = 40°
Step: 2
ABPQ = 105 = 21
Step: 3
ACPR = 126 = 21
Step: 4
⇒ ABPQ = ACPR and ∠A ≅ ∠P
Step: 5
SAS similarity theorem states that two triangles are similar if two sides in one triangle are in the same proportion to the corresponding sides in the other, and the included angles are equal.
Step: 6
Therefore, ΔABC ∼ ΔPQR by SAS similarity theorem.
Correct Answer is :   SAS similarity theorem
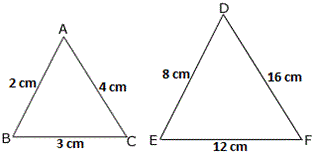
Q9Which theorem can prove ΔABC and ΔDEF similar?

A. AA similarity
B. SSS similarity theorem
C. SSA similarity theorem
D. SAS similarity theorem

Solutions
Share 
Step: 1
From the figure, we have ABDE = 28 = 14
Step: 2
BCEF = 312 = 14
Step: 3
ACDF = 416 = 14
Step: 4
⇒ ABDE = BCEF = ACDF
Step: 5
SSS similarity theorem states that if the corresponding sides of two triangles are proportional, then the triangles are similar.
Step: 6
Therefore, ΔABC ∼ ΔDEF by SSS similarity theorem.
Correct Answer is :   SSS similarity theorem
Q10Which of the following is/are true for two similar triangles ΔABC and ΔPQR?
I. ABPQ = BCQR = ACPR
II. ∠A = ∠B = ∠C = ∠P = ∠Q = ∠R
III. ABPQ = BCQR = ACPR = 1
IV. ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R.
A. I and IV only
B. II and III only
C. I only
D. III and IV only

Solutions
Share 
Step: 1
Two triangles are similar if and only if their corresponding angles are congruent and the measures of their corresponding sides are proportional.
  [By definition.]
Step: 2
ΔABC is similar to ΔPQR.
  [Given.]
Step: 3
Therefore, ABPQ = BCQR = ACPR, ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R.
Correct Answer is :   I and IV only

HighSchool Math