Solved Examples and Worksheet for Centre and Scale Factor in Dilation

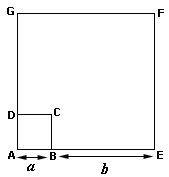
Q1The image of triangle ABC after dilation with respect to point A is A'B'C'. If AB = 12 in. and A'B' = 8 in., then find the scale factor.


A. 13
B. 32
C. 23
D. 12

Solutions
Share 
Step: 1
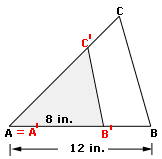
Scale factor = A'B'AB
= 812 = 23
  [Substitute the values and simplify.]
Step: 2
The scale factor is 23.
Correct Answer is :   23
Q2What is the scale factor that maps square ABCD to square AEFG?
[Given a = 2 and b = 8.]


A. 4
B. 10
C. 5
D. 14

Solutions
Share 
Step: 1
Scale factor = AEAB
Step: 2
= 2+82
Step: 3
= 102 = 5
Correct Answer is :   5
Q3Triangle ABC has the vertices as A(1, 2), B(- 3, 4) and C(- 4, - 2). Which of the following figures represents the triangle A′B′C′ dilated with a scale factor of 2 with center as A.


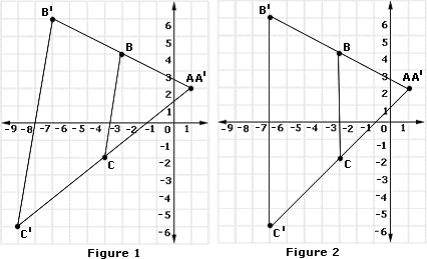
A. Figure 1
B. Figure 2

Solutions
Share 
Step: 1
Since the center of dilation is A, the image of A will be A itself. i.e., A and A′ coincides.
Step: 2
When B is dilated by scale factor of 2 with A as center, B will be the midpoint between A′ and B′.
Step: 3
Coordinates of B′ are (- 7, 6)
  [Apply midpoint formula.]
Step: 4
When C is dilated by scale factor of 2 with A as center, C will be the midpoint between A′ and C′.
Step: 5
Coordinates of C′ are (- 9, - 6)
  [Apply midpoint formula.]
Step: 6
A′B′C′ is plotted as shown in Figure 1.
Correct Answer is :   Figure 1
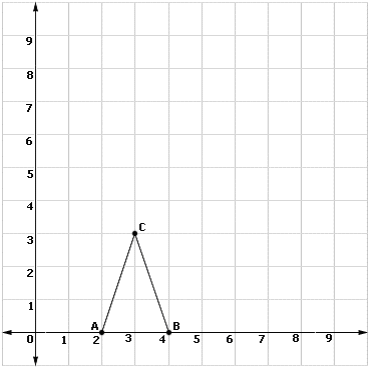
Q4Triangle ABC is shown in the figure. Find the vertices of the triangle under dilation with center as A and scale factor 3.

A. A′(6, 0), B′(8, 0) and C′(5, 9)
B. A′(6, 0), B′(12, 0) and C′(9, 9)
C. A′(2, 0), B′(12, 0) and C′(9, 9)
D. A′(2, 0), B′(8, 0) and C′(5, 9)

Solutions
Share 
Step: 1

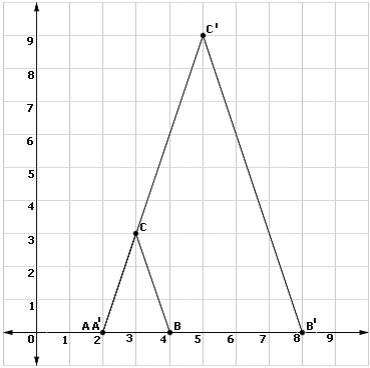
Step: 2
Image of A is A itself. A and A′ coincides.
Step: 3
Image of B is B′. AB′AB = 3
Step: 4
B divides AB′ in the ratio 1: 2
Step: 5
Coordinates of B′ are (8, 0).
Step: 6
Image of C is C′. AC′AC = 3
Step: 7
Coordinates of C′ are (5, 9).
  [Line segment formula.]
Correct Answer is :   A′(2, 0), B′(8, 0) and C′(5, 9)
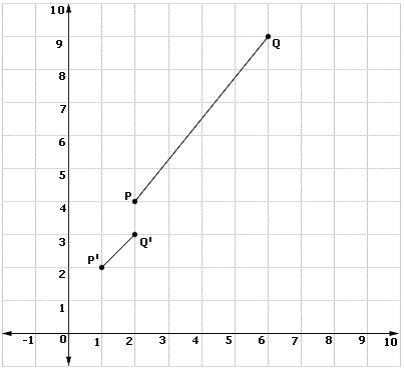
Q5Points P (2, 4) and Q (6, 9) on an XY plane are dilated to P′ and Q′ with the center as the origin. The scale factor of P is 12 and that of Q is 13. Find the difference between the lengths of the line segments PQ and P′Q′.


A. 41 -2
B. 2 -14
C. 2 -41
D. 14 -2

Solutions
Share 
Step: 1
P and Q are (2, 4) and (6, 9)
  [Given.]
Step: 2
P′ = (1, 2)
  [Multiply the coordinates by the scale factor.]
Step: 3
Q′ = (2, 3)
  [Multiply the coordinates by the scale factor.]
Step: 4
PQ = [(6 - 2)²  + (9 - 4)²] ]
  [Distance formula.]
Step: 5
= 41
  [Simplify.]
Step: 6
P′Q′ = [(2 - 1)²  + (3 - 2)² ]
  [Distance formula.]
Step: 7
P′Q′ = 2
  [Simplify.]
Step: 8
PQ - P′Q′ = 41 -2
  [Steps 5 and 7.]
Correct Answer is :   41 -2
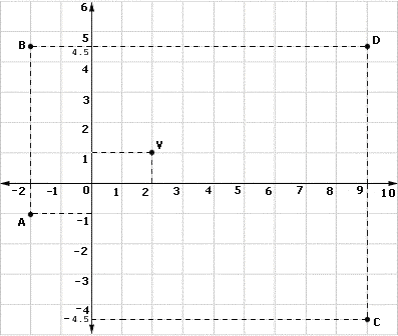
Q6Which among the following points is the image of point V under dilation with center as the origin and a scale factor of 4.5.


A. B
B. A
C. C
D. D

Solutions
Share 
Step: 1
Point V is (2, 1)
Step: 2
When it is under dilation with a scale factor of 4.5, the image will be (2 × 4.5, 1 × 4.5) = (9, 4.5)
Step: 3
This point is shown as D in the picture.
Correct Answer is :   D
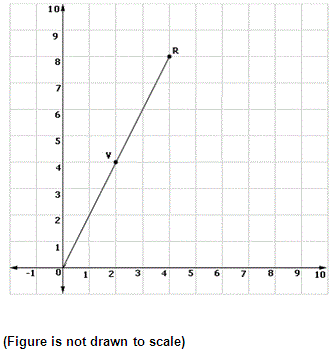
Q7Use a scale factor of 1.5 to dilate the line segment O-V-R. Find the coordinates of the point V after dilation with respect to the origin.

A. (3, 6)
B. (4, 8)
C. (2, 4)
D. (0, 0)

Solutions
Share 
Step: 1
Line segment O-V-R is dilated under a scale factor of 1.5 with origin as the center.
  [Given]
Step: 2
Co-ordinates of points O, V and R are (0, 0), (2, 4) and (4, 8) respectively.
Step: 3
To find the image of a point on the coordinate plane under a dilation with center as origin, multiply the co-ordinates with the scale factor.
Step: 4
Image of V (2, 4) = (2 × 1.5, 4 × 1.5)
Step: 5
= (3, 6)
  [Simplify]
Step: 6
Therefore, co-ordinates of the point V after dilation is (3,6).
Correct Answer is :   (3, 6)
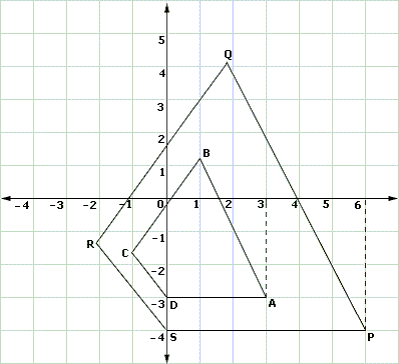
Q8The quadrilateral ABCD is a dilation of the quadrilateral PQRS with respect to C. The scale used in obtaining the dilated figure PQRS is 12. If AB || PQ, then what is AD parallel to?

A. SR
B. PQ
C. PS
D. QR

Solutions
Share 
Step: 1
Quadrilateral ABCD is the dilation of quadrilateral PQRS under a scale factor of 12
  [Given.]
Step: 2
AB | | PQ
  [Given.]
Step: 3
Images of vertices P, Q, R and S after dilation are A, B, C and D respectively.
Step: 4
So, AD || PS
  [Parallelism of lines of a figure does not change under dilation.]
Correct Answer is :   PS
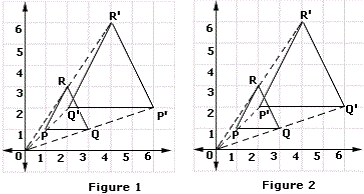
Q9Which of the figures show the dilation of the triangle PQR, with center as origin and with a scale factor of 2?


A. Figure 1
B. Figure 2

Solutions
Share 
Step: 1
Triangle PQR is dilated under a scale factor of 2 with origin as the center of dilation.
  [Given.]
Step: 2
Images of vertices P, Q and R after dilation are P′, Q′, and R′ respectively.
  [Orientation, i.e. the lettering order of a figure does not change under dilation.]
Step: 3
The triangle P′Q′R′ is the dilation of the triangle PQR with respect to the origin.
Step: 4
Therefore, figure 2 represents the dilation of the triangle PQR.
Correct Answer is :   Figure 2
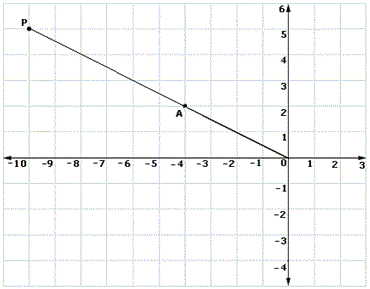
Q10Use a scale factor of 0.5 to dilate the line segment O-A-P with respect to the origin. If A′ and P′ are the images of the points A and P respectively, then what would be the relation between the points O, A′ and P′?

A. Non-collinear
B. Collinear

Solutions
Share 
Step: 1
Line segment O-A-P is dilated under a scale factor of 0.5 with origin as the center.
  [Given.]
Step: 2
Co-ordinates of points O, A and P are (0, 0), (-4, 2) and ( - 10, 5) respectively.
Step: 3
To find the image of a point on the coordinate plane under a dilation with center as origin, multiply the co-ordinates with the scale factor.
Step: 4
Image of A (- 4, 2) = (- 4 × 0.5, 2 × 0.5)
Step: 5
(-2, 1)
Step: 6
Image of P ( - 10, 5) = (- 10 × 0.5, 5 × 0.5)
Step: 7
( - 5, 2.5)
Step: 8
We notice that the points O, A′ and P′ are collinear
Step: 9
Therefore, the points O, A′ and P′ are collinear
Correct Answer is :   Collinear

HighSchool Math