Solved Examples and Worksheet for Areas of Triangles using Trigonometry

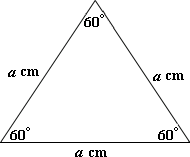
Q1What is the area of an equilateral triangle with side a cm? [Given a = 6.2 cm.]

A. 19.22 3 cm2
B. 12.4 3 cm2
C. 9.613 cm2
D. 6.23 cm2

Solutions
Share 
Step: 1
The side of the equilateral triangle is 4.8 cm.
Step: 2
Area of the equilateral triangle = (12) ×side length × side length × Sine of included angle.
  [Area of triangle given SAS.]
Step: 3
= 12× 4.8 × 4.8 × sin 60°
  [From the figure.]
Step: 4
= 12 × 23.04 × 32 = 5.763 cm2
Correct Answer is :   9.613 cm2
Q2Two side lengths of a triangle measure 6.3 cm and 8.4 cm. Choose the maximum area that the triangle can have.
A. 10.5 cm2
B. 52.92 cm2
C. 26.46 cm2
D. 8.4 cm2

Solutions
Share 
Step: 1
The sides of the triangle are 6.3 cm, 8.4 cm and let θ be the included angle of these sides.
  [Assuming θ as the included angle would help to find the area of the triangle]
Step: 2
Area of Triangle = 12× Side length × Side length × sine of included angle
  [Area of triangle given SAS.]
Step: 3
= (12)(6.3)(8.4) sin θ = 26.46 sinθ
  [Substitue to find the area]
Step: 4
sin θ has its maximum value 1, when θ = 90°.
Step: 5
The area of the given triangle is maximum when the included angle is 90°.
Step: 6
At θ = 90° the maximum value of A = 26.46 sin90° = 26.46(1) = 26.46 cm2.
  [Substitute the value of Sin 90° = 1]
Correct Answer is :   26.46 cm2
Q3Find the height of an equilateral triangle whose area is 93 in2.

A. 9 in
B. 3 in
C. 8 in
D. 7 in

Solutions
Share 
Step: 1
Let the side of the equilateral triangle be a in. and the height be h in. as shown.
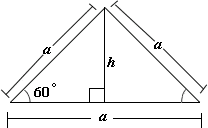
Step: 2
sin 60° = ha
  [Use the sine ratio.]
Step: 3
32=ha ⇒ a = 2h3
Step: 4
a = 2h3
  [Cross - product property.]
Step: 5
The area of the equilateral triangle = (12) × side length × side length × sin 60°.
  [Write the area of an equilateral triangle.]
Step: 6
= (12)(a)(a) sin 60° = (34)(4h23)
  [Substitute 2h3for a.]
Step: 7
= h23
  [Simplify.]
Step: 8
h23=93
  [The area of the equilateral triangle is given by 93 in2..]
Step: 9
h2 = 9
  [Simplify.]
Step: 10
h = 3 in.
  [Find square root on each side.]
Correct Answer is :   3 in
Q4Find the height of an equilateral triangle whose area is 253 in2.
A. 11 in
B. 10 in
C. 5 in
D. 9 in

Solutions
Share 
Step: 1
Let the side of the equilateral triangle be a in. and the height be h in. as shown.
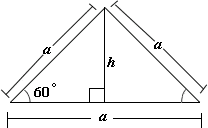
Step: 2
sin 60° = ha
  [Use the sine ratio.]
Step: 3
32=ha ⇒ a = 2h3
Step: 4
a = 2h3
  [Cross - product property.]
Step: 5
The area of the equilateral triangle = (12) × side length × side length × sin 60°.
  [Write the area of an equilateral triangle.]
Step: 6
= (12)(a)(a) sin 60° = (34)(4h23)
  [Substitute 2h3for a.]
Step: 7
= h23
  [Simplify.]
Step: 8
h23=253
  [The area of the equilateral triangle is given by 253 in2..]
Step: 9
h2 = 25
  [Simplify.]
Step: 10
h = 5 in.
  [Find square root on each side.]
Correct Answer is :   5 in
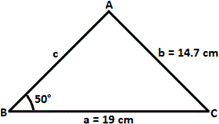
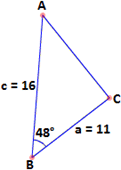
Q5In ΔABC, if a = 19 cm, b = 14.7 cm and ∠B = 50°, then what is the area of the triangle to four significant digits?


A. 103.8 cm2
B. 102.1 cm2
C. 121.2 cm2
D. 101.2 cm2

Solutions
Share 
Step: 1
Sin A19= Sin 50o14.7)
  [Use law of Sines: Sin Aa= Sin Bb.]
Step: 2
Sin A = 19 × Sin 50o14.7 )
Step: 3
Sin A ≈ 0.99012
  [Simplify.]
Step: 4
∠A = 82°
Step: 5
∠C = 180° - (∠A + ∠ B)
  [Triangle - Angle sum property.]
Step: 6
∠C = 180° - (82°+ 50°) = 48°
  [Substitute and simplify.]
Step: 7
Area of triangle ABC = 12 × a × b × Sin C
Step: 8
= 12× 19 × 14.7 × Sin 48° = 103.8
  [Substitute and simplify.]
Step: 9
Therefore, the area of the triangle ABC is ' 103.8 cm2 '.
Correct Answer is :    103.8 cm2
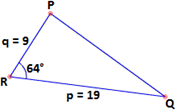
Q6In ΔPQR, if p = 19 cm, q = 9 cm and ∠R = 64°, then what is the area of the triangle to three significant digits?


A. 72.6 cm2
B. 68.5 cm2
C. 84.2 cm2
D. 76.8 cm2

Solutions
Share 
Step: 1
p = 19 cm, q = 9 cm and ∠ R = 64°
  [Given]
Step: 2
Area of triangle PQR = 12× p × q × Sin R
Step: 3
= 12× 19 × 9 × Sin 64° = 76.846
  [Substitute and simplify.]
Step: 4
Therefore, the area of the triangle PQR to three significant digits is 76.8 cm2.
Correct Answer is :   76.8 cm2
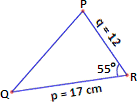
Q7In ΔPQR, if p = 17 cm, q = 12 cm and ∠R = 55°, then what is the area of the triangle to three significant digits?


A. 69.8 cm2
B. 83.6 cm2
C. 77.4 cm2
D. 89.1 cm2

Solutions
Share 
Step: 1
p = 17 cm, q = 12 cm and ∠R = 55°
  [Given]
Step: 2
Area of triangle PQR = 12× p × q × Sin R
Step: 3
= 12 × 17 × 12 × Sin 55° = 83.55
  [Substitute and simplify.]
Step: 4
Therefore, the area of the triangle PQR to three significant digits is 83.6 cm2.
Correct Answer is :   83.6 cm2
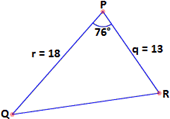
Q8In Δ PQR, if q = 13 cm, r = 18 cm and ∠P = 76°, then what is the area of the triangle to four significant digits?

A. 127.4 cm2
B. 109.8 cm2
C. 111.9 cm2
D. 113.5 cm2

Solutions
Share 
Step: 1
q = 13 cm, r = 18 cm and ∠ P = 76°
  [Given]
Step: 2
Area of triangle PQR = 12× q × r × Sin P
Step: 3
= 12× 13 × 18 × Sin 76° = 113.524
  [Substitute and simplify.]
Step: 4
Therefore, the area of the triangle PQR to four significant digits is 113.5 cm2.
Correct Answer is :   113.5 cm2
Q9In Δ ABC, if a = 11 cm, c = 16 cm and ∠B = 48°, then what is the area of the triangle to three significant digits?

A. 51.6 cm2
B. 65.4 cm2
C. 72.8 cm2
D. 58.9 cm2

Solutions
Share 
Q10Find the height of an equilateral triangle of area 753 cm2.

A. 25 cm
B. 15 cm
C. 9 cm
D. 12 cm

Solutions
Share 
Step: 1
Let the side of the equilateral triangle be a cm and the height be h cm as shown.
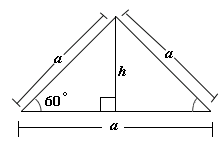
Step: 2
Sin 60° = ha.
  [Use the Sine ratio.]
Step: 3
32=ha⇒ a = 2h3
  [Substitute and simplify for a.]
Step: 4
Area of the equilateral triangle = 12× a × a × Sin 60°
Step: 5
12× 2h3 × 2h3 × 32 = h23 .
Step: 6
h23 = 753
  [The area of the equilateral triangle is given by 753 cm2.]
Step: 7
h2 = 753 × 3 = 75 × 3 = 225
  [Simplify]
Step: 8
h = 225 = 15
  [Apply square root on both sides]
Step: 9
Therefore, the height of the equilateral triangle is 15 cm.
Correct Answer is :   15 cm

HighSchool Math