Solved Examples and Worksheet for Solving Linear Systems Equations Graphically

Q1Using graphing method, find the number of solutions for the given linear system.
y = -x - 2
y = x + 2
A. No solution
B. Infinitely many solutions
C. Exactly one solution
D. None of the above

Solutions
Share 
Step: 1
y = -x - 2
  [Equation 1.]
Step: 2
y = x + 2
  [Equation 2.]
Step: 3
Graph both the equations using slope and y-intercept.
Step: 4
The two equations have different slopes.
Step: 5
It can be observed that both the lines intersect at only one point.
Step: 6
So, the linear system has exactly one solution.
Correct Answer is :   Exactly one solution
Q2Which of the following linear system matches the linear system shown in the graph?

A. 3y = - 2, y = 1
B. 3y = - 2x + 1, y = 1 - x
C. 3y = 2x, y = - x - 1
D. 3y = 2x, y = x - 1

Solutions
Share 
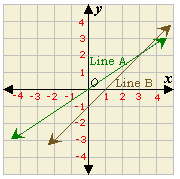
Step: 1
The equation of the line in slope-intercept form with slope m and y-intercept b is y = mx + b.
Step: 2
From the graph, y-intercept of line A is 0 and slope is 23.
Step: 3
The equation of the line A is y = 23x.
  [Substitute slope = 23 and y-intercept = 0 in the slope-intercept form equation.]
Step: 4
3y = 2x
  [Simplify.]
Step: 5
From the graph, the y-intercept of line B is - 1 and slope is 1.
Step: 6
The equation of the line B is y = x - 1.
  [Substitute slope = 1 and y-intercept = - 1 in the slope-intercept form equation.]
Step: 7
The linear system is
3y = 2x
y = x - 1.
Correct Answer is :   3y = 2x, y = x - 1
Q3Determine graphically whether the system of equations x = 5 and y = 8 is consistent and dependent, consistent and independent or inconsistent.
A. consistent and dependent
B. consistent and independent
C. inconsistent
D. cannot be determined

Solutions
Share 
Step: 1
x = 5
  [Equation 1.]
Step: 2
y = 8
  [Equation 2.]
Step: 3
Graph the equations.
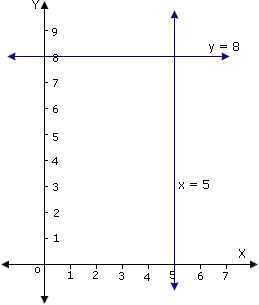
Step: 4
The lines are intersecting at a point (5, 8).
Step: 5
So, there is only one solution (5, 8).
Step: 6
Therefore, the system is consistent and independent.
Correct Answer is :   consistent and independent
Q4Use the graph shown to estimate the solution of the linear system.
y + x + 1 = 0
y + 3x - 1 = 0

A. (- 1, - 2)
B. (2, 1)
C. (1, - 2)
D. (1, 2)

Solutions
Share 
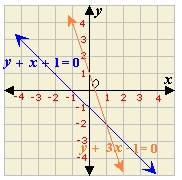
Step: 1
The two lines appear to intersect at the point (1, - 2).
Step: 2
Check the solution algebraically:
y + x + 1 = 0
  [Equation 1.]
Step: 3
(- 2) + 1 + 1 = 0
  [Substitute x = 1 and y = - 2 in equation 1.]
Step: 4
0 = 0
  [Simplify.]
Step: 5
y + 3x - 1 = 0
  [Equation 2.]
Step: 6
- 2 + 3(1) - 1 = 0
  [Substitute x = 1 and y = - 2 in equation 2.]
Step: 7
0 = 0
  [Simplify.]
Step: 8
The ordered pair (1, - 2) satisfies both the equations.
Step: 9
So, (1, - 2) is the solution of the linear system.
Correct Answer is :   (1, - 2)
Q5Solve by graphing. Confirm that the solutions obtained by graphing are correct by substituting them back into the original equations.
y = x
y = 4
A. (0, 0)
B. (0, 4)
C. (4, 4)
D. (4, 0)

Solutions
Share 
Step: 1
y = x
  [Equation 1.]
Step: 2
y = 4
  [Equation 2.]
Step: 3
Graph the equations.
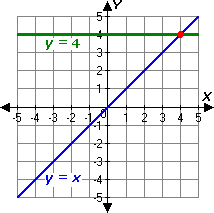
Step: 4
It appears that the two lines intersect at the point (4, 4).
  [From graph.]
Step: 5
Check the solution algebraically :
Step: 6
y = x
  [Equation 1.]
Step: 7
4 = 4, which is true.
  [Substitute x = 4 and y = 4.]
Step: 8
y = 4
  [Equation 2.]
Step: 9
4 = 4, which is true.
  [Substitute y = 4.]
Step: 10
So, (4, 4) is the solution of the linear system.
Correct Answer is :   (4, 4)
Q6Solve the linear system by graphing. Check the solution by using either substitution or elimination.
y = 2x + 1
x = - 1
A. (1, - 1)
B. (- 1, 1)
C. (1, 1)
D. (- 1, - 1)

Solutions
Share 
Step: 1
y = 2x + 1 ----- (1)
x = - 1 ----- (2)
  [Original system of equations.]
Step: 2
Graph the given equaions.
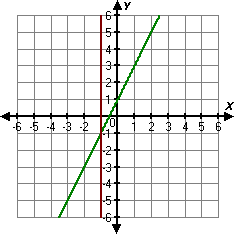
Step: 3
The graphical solution is (- 1, - 1).
Step: 4
Check the solution by substitution:
Use - 1 for x in equation (1).
Step: 5
y = 2(- 1) + 1
  [Substitute the values.]
Step: 6
y = - 1
  [Multiply and add.]
Step: 7
The exact solution is (- 1, - 1), which is same as graphical solution.
Correct Answer is :   (- 1, - 1)
Q7Use graph-and-check method to solve the linear system.
y = - x
x = 4

A. (4, - 4)
B. (- 4, 4)
C. (0, - 4)
D. (4, 0)

Solutions
Share 
Step: 1
y = - x
  [Equation 1.]
Step: 2
x = 4
  [Equation 2.]
Step: 3
Graph the equations.
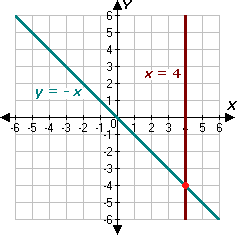
Step: 4
It appears that the two lines intersect at the point (4, - 4).
  [From graph.]
Step: 5
Check the solution algebraically :
Step: 6
y = - x
  [Equation 1.]
Step: 7
- 4 = - 4, which is true.
  [Substitute x = 4 and y = - 4.]
Step: 8
x = 4
  [Equation 2.]
Step: 9
4 = 4, which is true.
  [Substitute x = 4.]
Step: 10
So, (4, - 4) is the solution of the linear system.
Correct Answer is :   (4, - 4)
Q8Use graph-and-check method to solve the linear system.
y = 2x
y = - 4
A. (- 4, - 2)
B. (2, 4)
C. (- 2, - 4)
D. (- 2, 4)

Solutions
Share 
Step: 1
y = 2x
  [Equation 1.]
Step: 2
y = - 4
  [Equation 2.]
Step: 3
Graph the equations.
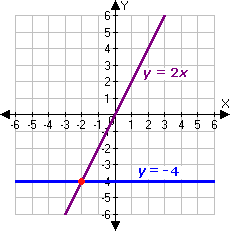
Step: 4
It appears that the two lines intersect at the point (- 2, - 4).
  [From graph.]
Step: 5
Check the solution algebraically :
Step: 6
y = 2x
  [Equation 1.]
Step: 7
- 4 = - 4, which is true.
  [Substitute x = - 2 and y = - 4.]
Step: 8
y = - 4
  [Equation 2.]
Step: 9
- 4 = - 4, which is true.
  [Substitute y = - 4.]
Step: 10
So, (- 2, - 4) is the solution of the linear system.
Correct Answer is :   (- 2, - 4)
Q9Identify the graph that represents the pair of linear equations.
2x + y = 1---- (1)
x + y = 2---- (2)


A. Graph 3
B. Graph 1
C. Graph 2
D. Graph 4

Solutions
Share 
Step: 1
Let us draw the graphs of the Equations (1) and (2). For this, we find two solutions of each of the equations, which are given in Tables.
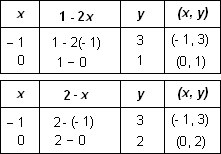
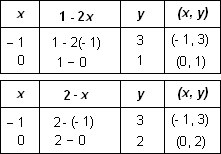
Step: 2
Plot the points A(- 1, 3), B(0, 1), P(- 1, 3) and Q(0, 2) on graph paper, and join the points to form the lines AB and PQ as shown in Figure.
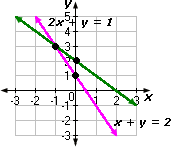
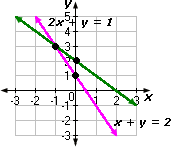
Step: 3
We observe that there is a point B (- 1, 3) common to both the lines AB and PQ. So, the solution of the pair of linear equations is x = - 1 and y = 3.
Correct Answer is :   Graph 1
Q10Find the solution of the simultaneous linear equations graphically.
3y = 2x
y = x - 1
A. (- 3, - 2)
B. (3, 2)
C. (- 3, 2)
D. (3, - 2)

Solutions
Share 
Step: 1
3y = 2x
y = x - 1
  [Given simultaneous linear equations.]
Step: 2
3y = 2x ⇒ y = 23x
Step: 3
When x = - 3, y = 23(- 3) = - 2
When x = 0, y = 23(0) = 0
When x = 3, y = 23(3) = 2
Step: 4
Thus, we get the following table:
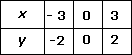
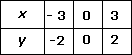
Step: 5
y = x - 1
Step: 6
When x = - 1, y = - 1 - 1 = - 2
When x = 0, y = 0 - 1 = - 1
When x = 3, y = 3 - 1 = 2.
Step: 7
Thus, we get the following table:
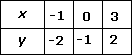
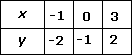
Step: 8
Plot the points on a graph paper.
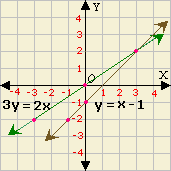
Step: 9
From the graph, the two lines intersect at (3, 2).
Step: 10
So, the solution for the given simultaneous linear equations is (3, 2).
Correct Answer is :   (3, 2)

HighSchool Math