Solved Examples and Worksheet for Representing Squares and Square Roots
A. + 19 and - 19
B. 19 and 20
C. +17 and -17
D. None of the above
Step: 1
[Original equation.]
Step: 2
[Apply square root on both sides.]
Step: 3
= ±( 1 9 × 1 9 )
[If y z y z
Step: 4
= ± 19
Step: 5
So, + 19 and - 19 are the two integers that satisfy the equation.
Correct Answer is : + 19 and - 19
A. $761
B. $786
C. $736
D. None of the above
Step: 1
Area of a square field = (side)2
Step: 2
side = A r e a
Step: 3
= 2 1 1 6
[Substitute.]
Step: 4
= 4 6 × 4 6
[Write 2116 as 46 × 46 and simplify.]
Step: 5
The perimeter of the square field = 4 × (side of the square field)
Step: 6
= 4 × 46 = 184
[Substitute and multiply.]
Step: 7
Cost of fencing the field = (Perimeter of the field) × (Cost of fencing per ft)
Step: 8
= 184 × 4 = 736
[Substitute and multiply.]
Step: 9
So, the cost of fencing the field is $736.
Correct Answer is : $736
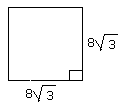
A. 156 square units
B. 192 square units
C. 133 square units
D. 145 square units
Step: 1
Area = length x width
[Formula.]
Step: 2
= 8√3 x 8√3
[Substitute the value of length and width.]
Step: 3
= 64 x 3
[Simplify.]
Step: 4
= 192
[Multiply.]
Step: 5
The area of the figure is 192 square units.
Correct Answer is : 192 square units
A. 6√3
B. 6/√3
C. 2/√3
D. 2√3
Step: 1
The area of the square = (side)2
[Formula.]
Step: 2
The side of the square = √(area of the square)
Step: 3
= √12
[Substitute the area of the square as 12.]
Step: 4
= √(2 x 2 x 3)
[Write 12 as a product of prime factors.]
Step: 5
= 2√3
[Find the square root.]
Step: 6
The side of the square with an area of 12 square units is 2√3 units.
Correct Answer is : 2√3
A. 37 and 74
B. 74 and -74
C. 37 and -37
D. None of the above
Step: 1
-y
[Original equation.]
Step: 2
[Divide each side by -1.]
Step: 3
[Apply square roots to each side.]
Step: 4
= ± 37
[Find the square root.]
Step: 5
The two integers that satisfy the equation -y
Correct Answer is : 37 and -37
A. 12 m
B. 14 m
C. 13 m
D. 15 m
Step: 1
Let n
Step: 2
The area of a square = side × side.
Step: 3
196 = n n
[Substitute the values.]
Step: 4
[Multiply.]
Step: 5
√n
[Square root each side.]
Step: 6
[Find the positive square root, since the side-length cannot be negative.]
Step: 7
The side-length of the square floor is 14 meters.
Correct Answer is : 14 m
A. 600 ft
B. 590 ft
C. 620 ft
D. 610 ft
Step: 1
The area of the school is in the form of square.
Step: 2
The area of the school = 22500 ft2
Step: 3
The side of the school = 2 2 5 0 0
[The side of square = a r e a o f t h e s q u a r e
Step: 4
= 1 5 0 × 1 5 0
[Write 22500 as perfect square.]
Step: 5
= 150
[Simplify.]
Step: 6
The perimeter of the school = 4 × 150
[The perimeter of the square = 4 × side of a square.]
Step: 7
= 600 ft.
[Simplify.]
Step: 8
The perimeter of the school is 600 ft.
Correct Answer is : 600 ft
A. 169
B. 256
C. 196
D. 225
E. 144
Step: 1
Units place digit is a square of a first odd prime number = 32 = 9.
Step: 2
10's place digit is a square root of a perfect square between 34 and 43 = 3 6
Step: 3
The three digit number is a perfect square.
Step: 4
So, the 3 digit number is 169.
Correct Answer is : 169
A. 16 m
B. 14 m
C. 17 m
D. 15 m
Step: 1
Let n
Step: 2
The area of a square = side × side.
Step: 3
256 = n n
[Substitute the values.]
Step: 4
[Multiply.]
Step: 5
[Square root each side.]
Step: 6
[Find the positive square root, since the side-length cannot be negative.]
Step: 7
The side-length of the square floor is 16 meters.
Correct Answer is : 16 m
A. 169
B. 225
C. 196
D. 144
E. 256
Step: 1
Units place digit is a square of a first odd prime number = 32 = 9.
Step: 2
10's place digit is a square root of a perfect square between 35 and 43 = 3 6
Step: 3
The three digit number is a perfect square.
Step: 4
So, the 3 digit number is 169.
Correct Answer is : 169
A. 9
B. 4.02
C. 5.16
D. 7
Step: 1
The length of Laura's old garden = 9 m
Step: 2
Area of garden = 9 × 9 = 81
[area of a square = side2]
Step: 3
Area of Laura's new garden = 1 5
Step: 4
Step: 5
Side length of the new garden = a r e a 1 6 . 2
[side = a r e a
Correct Answer is : 4.02 m
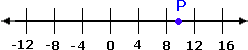
A.
B.
C.
D.
Step: 1
The perfect square nearer to 146 is 144.
Step: 2
[1 4 4
Step: 3
The perfect square nearer to 62 is 64.
Step: 4
[6 4
Step: 5
The perfect square nearer to 8 is 9.
Step: 6
[9
Step: 7
The perfect square nearer to 98 is 100.
Step: 8
[1 0 0
Step: 9
So, the point P represents 9 8
Correct Answer is : 9 8
A. 32 square inches
B. 64 square inches
C. 16 square inches
D. 8 square inches
Step: 1
Area of the square = side2 = 16 square inches
[Given.]
Step: 2
Side = 4 inches
[Take square root on both sides of the equation and simplify.]
Step: 3
Double the length of the side = 2 × 4 inches = 8 inches
Step: 4
The area of the new square = 8 in. × 8 in. = 64 in.2
Correct Answer is : 64 square inches
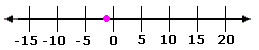
A. -
B.
C. -
D.
Step: 1
The point on the line lies between 0 and - 5 .
Step: 2
Among the choices - 6 8
[The point lie left to the 0 on the number line.]
Step: 3
The point on the number line is closer to 0.
Step: 4
Among the choices the approximate value of - 6
Step: 5
So, the point on the number line represents - 6
Correct Answer is : - 6
- Converting Numbers to Standard and Scientific Notation-Gr 8-Solved Examples
- Comparing and Ordering Numbers in Scientific Notation-Gr 8-Solved Examples
- Operations with Scientific Notations-Gr 8-Solved Examples
- Using Laws of Exponents-Gr 8-Solved Examples
- Identifying Square and Cube Roots of a Numbers-Gr 8-Solved Examples
- Applying Proportional Relationships-Gr 8-Solved Examples
- Using Graphs to represent Proportional Relationships-Gr 8-Solved Examples
- Solving Linear Equations in One Variable-Gr 8-Solved Examples
- Solving Multi-Step Linear Equations Using Distributive Property-Gr 8-Solved Examples
- Solving Systems of Equations by Substitution Method-Gr 8-Solved Examples
- Solving Systems of Equations by Elimination Method-Gr 8-Solved Examples
- Solving Linear Systems Equations Graphically-Gr 8-Solved Examples
- Finding Number of Solutions of System of Linear Equations-Gr 8-Solved Examples
- Word Problems on Systems of Equations-Gr 8-Solved Examples
Related Worksheet
- Square Root