Triangle Inequality Theorem-Geometry-Solved Examples

Solved Examples and Worksheet for Triangle Inequality Theorem

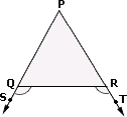
Q1Sides PQ and PR are produced and ∠SQR > ∠TRQ. What is the relationship between PQ and PR?

A. PQ > PR
B. PQ < PR
C. PQ = 2PR
D. PQ = PR

Solutions

Step: 1

∠SQR = 180^o - (∠PQR)

[∠SQP is a straight angle.]

Step: 2

∠TRQ = 180^o - (∠PRQ)

[∠TRP is a straight angle.]

Step: 3

180^o - (∠PQR) > 180^o - (∠PRQ)

[∠SQR > ∠TRQ.]

Step: 4

∠PRQ > ∠PQR

[Simplify.]

Step: 5

PQ > PR

[In a triangle the side opposite to the greater angle is greater.]

Correct Answer is : PQ > PR

Q2Arrange the angles of ΔABC in descending order.

A. m∠C > m∠A > m∠B
B. m∠A > m∠B > m∠C
C. m∠B > m∠A > m∠C
D. m∠C > m∠B > m∠A

Solutions

Step: 1

In a scalene triangle, the angle opposite to the larger side is larger.

Step: 2

As 14 > 11 > 8, we have m∠C > m∠B > m∠A

Correct Answer is : m∠C > m∠B > m∠A

Q3The side lengths of a triangle are 5 cm, 7 cm and z cm respectively. Which of the following is true?

A. 2 < z < 12
B. 5 < z < 12
C. 5 < z < 7
D. 7 < z < 12

Solutions

Step: 1

z < 5 + 7

[Triangle Inequality Theorem.]

Step: 2

z < 12

[In a triangle the difference of any two sides is less than the third side.]

Step: 3

z > 7 - 5

Step: 4

z > 2

Step: 5

2 < z < 12

[Step 2 and step 4.]

Correct Answer is : 2 < z < 12

Q4Which of the following can be the length of BC?

A. 9 cm
B. 5 cm
C. 2 cm
D. 23 cm

Solutions

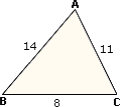
Step: 1

BC < 14 + 9

[Triangle Inequality Theorem.]

Step: 2

BC < 23 cm

Step: 3

BC > 14 - 9

[In a triangle, the difference of the lengths of any two sides is less than the third side.]

Step: 4

BC > 5 cm

Step: 5

5 cm < BC < 23 cm

Step: 6

As 9 lies between 5 and 23, BC can be 9 cm.

Correct Answer is : 9 cm

Q5Which of the following can be the length of BC?

A. 11 cm
B. 14 cm
C. 23 cm
D. 6 cm

Solutions

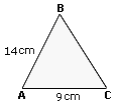
Step: 1

BC < 17 + 6

[Triangle Inequality Theorem.]

Step: 2

BC < 23 cm

Step: 3

BC > 17 - 6

[In a triangle, the difference of the lengths of any two sides is less than the third side.]

Step: 4

BC > 11 cm

Step: 5

11 cm < BC < 23 cm

Step: 6

From the values given in the options, 14 cm lies between 11 cm and 23 cm.

Step: 7

So, the length of BC is 14 cm.

Correct Answer is : 14 cm

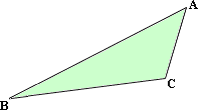
Q6AB > BC > CA. What could be the measures of ∠A, ∠B and ∠C respectively?

A. 30, 40, 110
B. 30, 110, 40
C. 40, 30, 110
D. 110, 40, 30

Solutions

Step: 1

AB > BC > CA ⇒ ∠C > ∠A > ∠B

[In a triangle, the greater angle is opposite to the greater side.]

Step: 2

Option (C) satisfies the above condition as for m∠A = 40, m∠B = 30 and m∠C = 110, ∠C > ∠A > ∠B.

Correct Answer is : 40, 30, 110

Q7In a triangle, the smallest angle is 40^o. The largest angle is

A. 139^o
B. 99^o
C. less than 100^o
D. greater than 100^o

Solutions

Step: 1

Smallest angle + medium angle + largest angle = 180^o

[Triangle-Angle-Sum theorem.]

Step: 2

40^o + (Medium angle) + (Largest angle) = 180^o

[Substitute.]

Step: 3

Medium angle = 140 - (largest angle)

[Simplify.]

Step: 4

Medium angle > smallest angle

Step: 5

140 - (largest angle) > 40^o

[Step 3.]

Step: 6

Largest angle < 100^o

[Simplify.]

Correct Answer is : less than 100^o

Q8In ΔABC, p cm and h cm are the perimeter and the sum of the altitudes of the triangle. Then what is the relationship between p and h?
A. p = 2h
B. p < h
C. p > h
D. p = h

Solutions

Step: 1

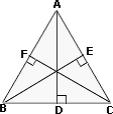
Step: 2

In ΔADB, AB > AD

[In a right triangle, hypotenuse is the longest side.]

Step: 3

Similarly, BC > BE and CA > CF

Step: 4

AB + BC + CA > AD + BE + CF

[Add the three inequalities above.]

Step: 5

p > h

Correct Answer is : p > h

Q9In ΔABC, let p cm and r cm denote the perimeter and the sum of its medians respectively. What is the relationship between p and r?
A. p > r
B. p = 2r
C. p < r
D. p = r

Solutions

Step: 1

Let a, b, c be the length of the sides and m₁, m₂, m₃ be the length of the medians.

Step: 2

[Produce AD to E such that AD = DE and join C to E.]

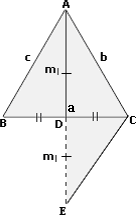
Step: 3

ΔBDA ≅ ΔCDE

[SAS postulate.]

Step: 4

CE = BA = c

[Step 3.]

Step: 5

In ΔAEC, AC + CE > AE

[Triangle Inequality Theorem.]

Step: 6

b + c > 2m₁

[Substitute.]

Step: 7

Similarly, for other medians, we get c + a > 2m₂ and a + b > 2m₃

Step: 8

(b + c) + (c + a) + (a + b) > 2m₁ + 2m₂ + 2m₃

[Add the three inequalities.]

Step: 9

2(a + b + c) > 2(m₁ + m₂ + m₃)

[Add.]

Step: 10

(a + b + c) > m₁ + m₂ + m₃

[Simplify.]

Step: 11

p > r

Correct Answer is : p > r

Q10In ΔABC, ∠A = 68^o, ∠B = 52^o. Which is the greatest side?
A. AB
B. BC
C. CA
D. cannot be determined with the given data

Solutions

Step: 1

In ΔABC, ∠C = 180^o - (∠A + ∠B)

[Triangle Angle Sum theorem.]

Step: 2

∠C = 180^o - (68^o + 52^o)

[Substitute.]

Step: 3

∠C = 60^o

[Substitute.]

Step: 4

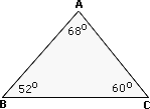
Step: 5

∠A is the greatest angle ⇒ BC is the greatest side.

[In a triangle, the greatest side is opposite to the greatest angle.]

Correct Answer is : BC

Q11In a triangle, which is the side opposite to the obtuse angle?
A. the smallest
B. neither the greatest nor the smallest
C. either the greatest or the smallest
D. the greatest

Solutions

Step: 1

An obtuse angle is the greatest angle in the triangle.

[Triangle-Angle-Sum theorem.]

Step: 2

Side opposite to the greatest angle i.e., the obtuse angle is the greatest.

Correct Answer is : the greatest

Q12In ΔPQR, PQ = PR, ∠Q = 65^o. Find the relationship between QR and PR.
A. QR = PR
B. QR = 2PR
C. QR < PR
D. QR > PR

Solutions

Step: 1

∠R = ∠Q = 65^o

[As PQ = PR.]

Step: 2

∠P = 180^o - (∠R + ∠Q)

[Triangle Angle Sum theorem.]

Step: 3

∠P = 180^o - (65^o + 65^o)

[Substitute.]

Step: 4

∠P = 50^o

[Simplify.]

Step: 5

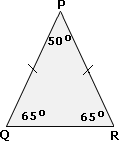
Step: 6

PR > QR

[In a triangle, the side opposite to the greater angle is greater.]

Step: 7

QR < PR

Correct Answer is : QR < PR

Q13In ΔABC, m∠A = 42, m∠B = 78. What is the relationship between AC and AB?
A. AC < AB
B. AC = AB
C. AC > AB
D. AC = 2AB

Solutions

Step: 1

∠C = 180^o - (∠A + ∠B)

[Triangle-Angle-Sum theorem.]

Step: 2

∠C = 180^o - (42^o + 78^o)

[Substitute.]

Step: 3

∠C = 60^o

[Simplify.]

Step: 4

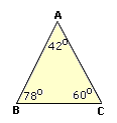
Step: 5

∠B > ∠C ⇒ AC > AB

[In a triangle, the greater side is opposite to the greater angle.]

Correct Answer is : AC > AB

Q14In ΔXYZ, ∠X = 42^o and ∠Y = 52^o. The bisectors of ∠X and ∠Y meet at O. Which of the following is true?

A. OY = 2OX
B. OY = OX
C. OY < OX
D. OY > OX

Solutions

Step: 1

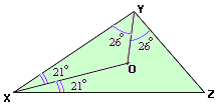
Step: 2

In ΔXOY, ∠OYX > ∠OXY ⇒ OX > OY

[In a triangle the greater side is opposite to the greater angle.]

Step: 3

OY < OX.

Correct Answer is : OY < OX

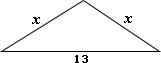
Q15In the figure, x is a whole number. What is the smallest possible value for x?

A. 1 unit
B. 7 units
C. 6 units
D. 12 units

Solutions

Step: 1

2x > 13

[Sum of two sides shall be greater than the third side.]

Step: 2

Minimum value of x shall be 7 units.

[x is to be a whole number.]

Correct Answer is : 7 units

Solved Examples and Worksheet for Triangle Inequality Theorem

Related Worksheet

Related Topic

HighSchool Math