Solved Examples and Worksheet for Area and Volume Measures using Scale Factors

Q1A parking lot is in the shape of a square measuring 19 ft by 12 ft. If you extend it by a scale factor of 3.5, find the new area of the parking lot.
A. 228 ft2
B. 235 ft2
C. 798 ft2
D. 2793 ft2

Solutions
Share 
Step: 1
New area of the parking lot = Area of the original parking lot × (scale factor)2
  [Increasing the length of a side of an object by factor x increases the area by factor x2 .]
Step: 2
= (19 × 12) × (3.5)2
Step: 3
= 2793 ft2
Step: 4
Therefore, the new area of the parking lot is 2793 ft2.
Correct Answer is :   2793 ft2
Q2A lawn is in the shape of a rectangle measuring 12 ft by 7 ft. If you extend the lawn by a scale factor of 2, what will be the new area of the lawn?

A. 336 ft2
B. 320 ft2
C. 340 ft2
D. 200 ft2

Solutions
Share 
Q3A park is in the shape of a square measuring 16 ft by 16 ft. If you extend the lawn by a scale factor of 4, what will be the new area of the park?

A. 3096 ft2
B. 4096 ft2
C. 3960 ft2
D. 4906 ft2

Solutions
Share 
Q4A lawn is in the shape of a rectangle measuring 17 ft by 15 ft. If you extend it by a scale factor of 3, find the new area of the lawn.

A. 2095 ft2
B. 495 ft2
C. 2295 ft2
D. 1295 ft2

Solutions
Share 
Step: 1
New area of the lawn = Area of the original lawn × (scale factor)2
  [Increasing the length of a side of an object by factor x increases the area by factor x2 .]
Step: 2
= (17 × 15) × (3)2
Step: 3
= 2295 ft2
Step: 4
Therefore, the new area of the lawn is 2295 ft2.
Correct Answer is :   2295 ft2
Q5A ground is in the shape of a square measuring 15 ft by 15 ft. If you extend it by a scale factor of 4, find the new area of the ground.

A. 4805 ft2
B. 3800 ft2
C. 3600 ft2
D. 1800 ft2

Solutions
Share 
Step: 1
New area of the ground = Area of the original ground × (scale factor)2
  [Increasing the length of a side of an object by factor x increases the area by factor x2 .]
Step: 2
= (15 × 15) × (4)2
Step: 3
= 3600 ft2
Step: 4
Therefore, the new area of the ground is 3600 ft2.
Correct Answer is :   3600 ft2
Q6A field is in the shape of a rectangle measuring 24 ft by 18 ft. If you extend it by a scale factor of 2.5, find the new area of the field.

A. 2856 ft2
B. 2700 ft2
C. 1700 ft2
D. 2568 ft2

Solutions
Share 
Step: 1
New area of the field = Area of the original field × (scale factor)2
  [Increasing the length of a side of an object by factor x increases the area by factor x2 .]
Step: 2
= (24 × 18) × (2.5)2
Step: 3
= 2700 ft2
Step: 4
Therefore, the new area of the field is 2700 ft2.
Correct Answer is :   2700 ft2
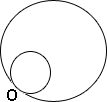
Q7In the figure, the bigger circle is the image of the smaller circle under an enlargement with centre O and scale factor 4. Given that the area of the larger circle is 80 cm2. Calculate the area of the smaller circle.

A. 5 cm2
B. 20 cm2
C. 320 cm2
D. 1280 cm2

Solutions
Share 
Step: 1
Area of the larger circle = 80 cm2
Scale factor of the enlargement, k = 4
Step: 2
Area of object = Area of image ÷ k2
Step: 3
Area of the smaller circle = Area of the larger circle ÷ k2
Step: 4
= 80 ÷ 42
  [Substitute the values.]
Step: 5
= 80 ÷ 16
= 5
  [Divide.]
Step: 6
Therefore, the area of the smaller circle is 5 cm2.
Correct Answer is :   5 cm2
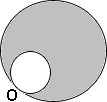
Q8In the figure, a circular garden of area 20 cm2 is enlarged by a scale of 3.5, with centre of enlargement O. Calculate the area of the shaded region.


A. 90 cm2
B. 265 cm2
C. 225 cm2
D. 50 cm2

Solutions
Share 
Step: 1
Area of the circular garden = 20 cm2
Step: 2
Scale factor of the enlargement, k = 3.5
Step: 3
Area of image = k2 × Area of the object
Step: 4
Area of the enlarged garden = Area of the original garden × k2
Step: 5
= 20 × 3.52
  [Substitute the values.]
Step: 6
= 20 × 12.25
= 245cm2
  [Multiply.]
Step: 7
Area of the shaded region = Area of the enlarged garden - Area of the original garden
Step: 8
= 245 - 20
= 225
  [Substitute the values and subtract.]
Step: 9
Therefore, the area of the shaded region is 225 cm2.
Correct Answer is :   225 cm2

HighSchool Math