Solved Examples and Worksheet for Identifying Conic Sections

Q1Which conic section is modeled by the equation x2 + y2 = 81?

A. an ellipse
B. a circle
C. a parabola
D. a hyperbola

Solutions
Share 
Step: 1
x2 + y2 = 81
  [Equation of conic.]
Step: 2
x2 + (0)2 = 81
  [Replace y = 0 to find the x - intercept.]
Step: 3
x2 = 81
  [Simplify.]
Step: 4
x = 9 or - 9
  [Solve for x.]
Step: 5
So, the x - intercepts of the graph are (- 9, 0) and (9 , 0).
Step: 6
(0)2 + y2 = 81
  [Replace x = 0 to find the y - intercept.]
Step: 7
y = 9 or y = - 9
  [Solve for y.]
Step: 8
So, the y - intercepts of the graph are (0, - 9) and (0, 9).
Step: 9
The equation x2 + y2 = 81 models a circle, since the intercepts are equidistant from the center, whcih is the origin.
Correct Answer is :   a circle
Q2Which conic section is modeled by the equation 9x2 + 16y2 = 144 ?
A. a hyperbola
B. an ellipse
C. a circle
D. a parabola

Solutions
Share 
Step: 1
9x2 + 16y2 = 144
  [Equation of conic.]
Step: 2
9x2 + 16(0)2 = 144
  [Replace y = 0 to find the x - intercept.]
Step: 3
x2 = 16
  [Simplify.]
Step: 4
x = 4 or x = - 4
  [Solve for x.]
Step: 5
So, the x - intercepts of the graph are (- 4, 0) and (4, 0).
Step: 6
9(0)2 + 16y2 = 144
  [Replace x = 0 to find the y - intercept.]
Step: 7
y2 = 9
  [Simplify.]
Step: 8
y = 3 or - 3
  [Solve for y.]
Step: 9
So, the y - intercepts of the graph are (0, - 3) and (0, 3).
Step: 10
The equation 9x2 + 16y2 = 144 models an ellipse, since the intercepts are not equidistant from the center, which is the origin.
Correct Answer is :   an ellipse
Q3Choose the conic section modeled by the equation x2 - y2 = 144.

A. an ellipse
B. a hyperbola
C. a circle
D. a parabola

Solutions
Share 
Step: 1
x2 - y2 = 144
  [Equation of conic.]
Step: 2
x2 - (0)2 = 144
  [Replace y = 0 to find the x - intercept.]
Step: 3
x2 = 144
  [Simplify.]
Step: 4
x = 12 or x = - 12
  [Solve for x.]
Step: 5
So, the x - intercepts of the graph are (- 12, 0) and (12, 0).
Step: 6
(0)2 - y2 = 144
  [Replace x = 0 to find the y - intercept.]
Step: 7
y2 + 144 = 0
  [Simplify.]
Step: 8
The y - intercepts of the graph does not exist, since the equation y2 + 144 = 0 has no real solutions.
  [Discriminant of the quadratic equation is negative.]
Step: 9
The given conic section models a hyperbola, since it has one pair of intercepts (- 12, 0) and (12, 0).
Correct Answer is :   a hyperbola
Q4If a right circular cone is cut with a plane perpendicular to the axis of the cone, then what is the resultant cross section?

A. A cylinder
B. An ellipse
C. A parabola
D. A circle

Solutions
Share 
Step: 1
The plane is perpendicular to the axis of the cone. So, the resultant cross section will be a circle.
Correct Answer is :   A circle
Q5If Andy threw a ball straight up, then what shape would the graph of height of the ball verses time be?

A. ellipse
B. circular
C. parabola
D. hyperbola

Solutions
Share 
Step: 1
The path of the ball is a parabola.
Step: 2
The height of the ball begins at the lowest point.
Step: 3
The ball gets higher and slower, then eventually stops at the peak. Then the ball slowly descends and picks up speed until it hits the ground.
Step: 4
Since it has one peak where the ball stops and the slope is zero, it has to be a parabola.
Correct Answer is :    parabola
Q6What is the graph of the equation represented by y2 - 4x - 6y + 21 = 0?
A. circle
B. parabola
C. hyperbola
D. ellipse

Solutions
Share 
Step: 1
y2 - 4x - 6y + 21 = 0
Step: 2
y2 - 6y = 4x - 21
  [Seperate the y terms.]
Step: 3
y2 - 6y + 9 = 4x - 21 + 9
  [Complete the square.]
Step: 4
(y - 3)2 = 4(x - 3)
Step: 5
This equation is in the standard form (y - k)2 = 4p(x - h), where h = 3, k = 3, and p = 44 = 1, which represents a parabola.
Correct Answer is :   parabola
Q7Which of the following statement is true?
A. A Conic section is the intersection of a plane and a sphere.
B. A Conic section is the intersection of a plane and a cone.
C. A Conic section is the intersection of two cones.
D. A Conic section is the intersection of a line and a cone.

Solutions
Share 
Step: 1
The correct statement is, 'A Conic section is the intersection of a plane and a cone'
Correct Answer is :   A Conic section is the intersection of a plane and a cone.
Q8The intersection of a right circular cone with a plane parallel to an element of the cone generates a plane curve known as
A. a hyperbola
B. a circle
C. an ellipse
D. a parabola

Solutions
Share 
Step: 1
The intersection of a right circular cone with a plane parallel to an element of the cone generates a plane curve known as a parabola.
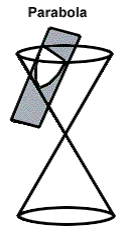
Correct Answer is :   a parabola
Q9If no line of the cone is parallel to the plane which is intersecting the cone, then the intersection is a closed curve known as
A. a circle
B. a semicircle
C. an ellipse
D. a parabola

Solutions
Share 
Step: 1
If no line of the cone is parallel to the plane, the intersection is a closed curve, known as an ellipse.
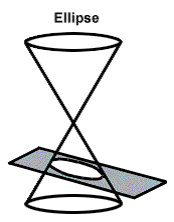
Correct Answer is :   an ellipse
Q10A plane curve having two branches, formed by the intersection of a plane with both halves of a right circular cone at an angle parallel to the axis of the cone known as

A. a hyperbola
B. an ellipse
C. a parabola
D. a circle

Solutions
Share 
Step: 1
A plane curve having two branches, formed by the intersection of a plane with both halves of a right circular cone at an angle parallel to the axis of the cone known as a hyperbola.
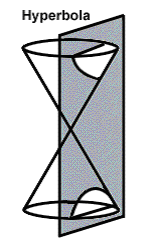
Correct Answer is :   a hyperbola

HighSchool Math