Solved Examples and Worksheet for Graphing Conic Sections
A.
B.
C.
D.
Step: 1
Step: 2
[Take out the common factor.]
Step: 3
[Add and subtract (4 2
Step: 4
[Rewrite the equation.]
Step: 5
[Simplify.]
Step: 6
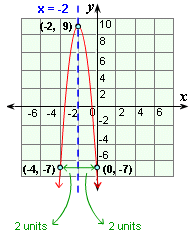
The vertex is (- 2, 9).
The axis of symmetry is the line with the equation x
Step: 7
Plot the vertex and draw the axis of symmetry.
Step: 8
Find another point.
Step: 9
When x y
Step: 10
The reflection of (0, - 7) is (- 4, - 7).
Plot it.
Step: 11
Connect the points with a smooth curve.

Correct Answer is : y x
A.
B.
C.
D.
Step: 1
Step: 2
Step: 3
[Add and subtract (4 2
Step: 4
[Rewrite the equation.]
Step: 5
[Simplify.]
Step: 6
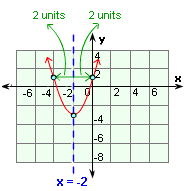
The vertex is (- 2, - 3).
The axis of symmetry is the line with the equation x
Step: 7
Plot the vertex and draw the axis of symmetry.
Step: 8
Find another point.
Step: 9
When x y
Step: 10
The reflection of (0, 1) is (- 4, 1).
Plot it.
Step: 11
Connect the points with a smooth curve.

Correct Answer is : y x
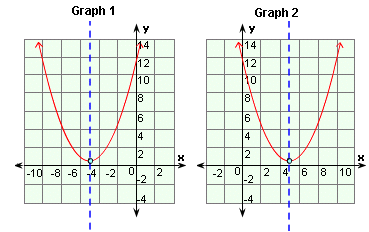
A.
B.
C.
D.
Step: 1
Step: 2
[Take out the common factor.]
Step: 3
[Add and subtract (- 10 2
Step: 4
[Rewrite the equation.]
Step: 5
[Simplify.]
Step: 6
[Simplify.]
Step: 7
The vertex is (5, 1 2 x
Step: 8
Plot the vertex and draw the axis of symmetry.
Step: 9
Find another point.
Step: 10
When x y 23 50 1 2 23 2 1 2
Step: 11
The reflection of (0, 12) is (10, 12).
Plot it.
Step: 12
Connect the points with a smooth curve.
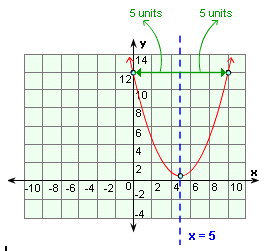

Correct Answer is : y 23 50 x 1 2
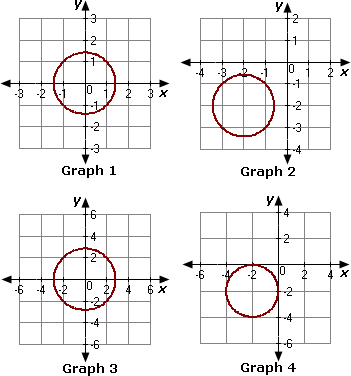
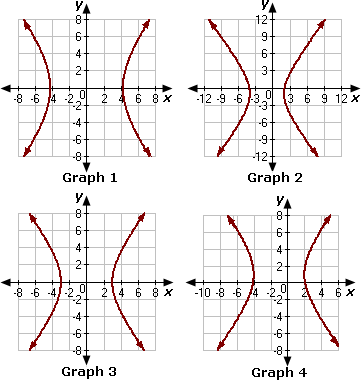
A. Graph 4
B. Graph 1
C. Graph 2
D. Graph 3
Step: 1
[Given.]
Step: 2
The general form of the equation of the circle is (x h y k r x y h k r
Step: 3
Compare the given equation with the general form of the circle equation.
Step: 4
(h k
Step: 5
Step: 6
[Take square root on both sides of the equation.]
Step: 7
From the given graphs, we can observe that the circle in Graph 1 has centre as origin and radius as 1.4.
Step: 8
Therefore, Graph 1 represents the given equation of the circle.
Correct Answer is : Graph 1
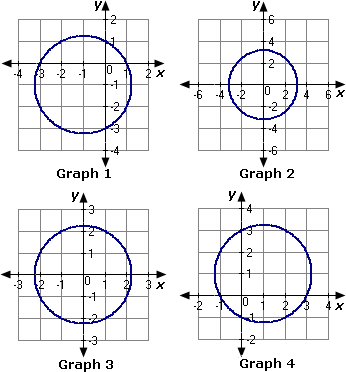
A. Graph 4
B. Graph 1
C. Graph 2
D. Graph 3
Step: 1
[Given.]
Step: 2
The general form of the equation of the circle is (x h y k r x y h k r
Step: 3
Compare the given equation with the general form of the circle equation.
Step: 4
(h k
Step: 5
Step: 6
[Take square root on both sides of the equation.]
Step: 7
From the given graphs, we can observe that the circle in Graph 2 has centre as origin and radius as 2.7.
Step: 8
Therefore, Graph 2 represents the given equation of the circle.
Correct Answer is : Graph 2
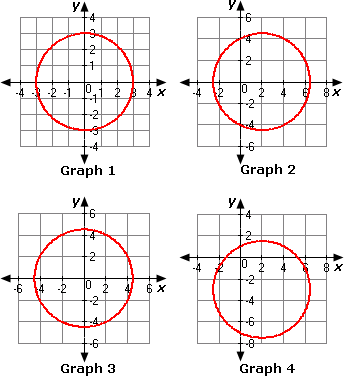
A. Graph 2
B. Graph 3
C. Graph 4
D. Graph 1
Step: 1
[Given.]
Step: 2
The general form of the equation of the circle is (x h y k r x y h k r
Step: 3
Compare the given equation with the general form of the circle equation.
Step: 4
(h k
Step: 5
Step: 6
[Take square root on both sides of the equation.]
Step: 7
From the given graphs, we can observe that the circle in Graph 1 has centre as origin and radius as 3.
Step: 8
Therefore, Graph 1 represents the given equation of the circle.
Correct Answer is : Graph 1
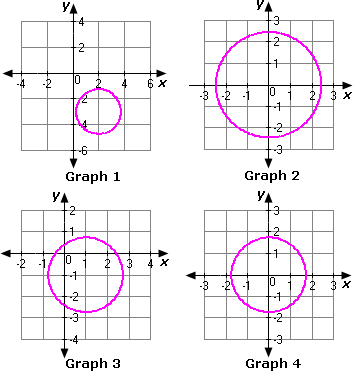
A. Graph 4
B. Graph 1
C. Graph 3
D. Graph 2
Step: 1
[Given.]
Step: 2
The general form of the equation of the circle is (x h y k r x y h k r
Step: 3
Compare the given equation with the general form of the circle equation.
Step: 4
(h k
Step: 5
Step: 6
[Take square root on both sides of the equation.]
Step: 7
From the given graphs, we can observe that the circle in Graph 2 has centre as origin and radius as 2.4.
Step: 8
Therefore, Graph 2 represents the given equation of the circle.
Correct Answer is : Graph 2
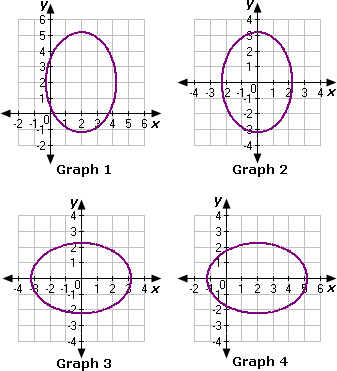
A. Graph 1
B. Graph 3
C. Graph 2
D. Graph 4
Step: 1
[Given.]
Step: 2
The standard form of the equation of ellipse is ( x - h ) 2 a 2 ( y - k ) 2 b 2
[(x y h k
Step: 3
Compare the given equation with the standard form of the equation of ellipse.
Step: 4
The center of the ellipse is at (0, 0).
Step: 5
Step: 6
[Take square root on both sides of the equation.]
Step: 7
Step: 8
[Take square root on both sides of the equation.]
Step: 9
Length of the major axis = 2a
= 21 0
= 2
Step: 10
Length of the minor axis = 2b
= 25
= 2
Step: 11
[Relation between a b c
Step: 12
Step: 13
[Take square root on both sides of the equation.]
Step: 14
So, the foci of the ellipse are (5 5
[The foci of the ellipse are (c c
Step: 15
From the given graphs, we can observe that the ellipse in Graph 2 have center at the origin, foci as (5 5 1 0 5 x 1 0 y 5
Step: 16
Therefore, Graph 2 represents the given equation of the ellipse.
Correct Answer is : Graph 2
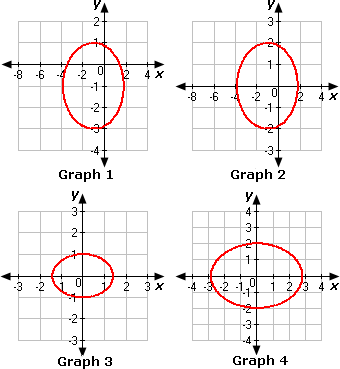
A. Graph 2
B. Graph 3
C. Graph 4
D. Graph 1
Step: 1
4x 2 y 2
[Given.]
Step: 2
[Divide both sides of the equation by 32.]
Step: 3
The standard form of the equation of ellipse is ( x - h ) 2 a 2 ( y - k ) 2 b 2
[(x y h k
Step: 4
Compare the given equation with the standard form of the equation of ellipse.
Step: 5
The center of the ellipse is at (0, 0).
Step: 6
Step: 7
[Take square root on both sides of the equation.]
Step: 8
Step: 9
[Take square root on both sides of the equation.]
Step: 10
Length of the major axis = 2a
= 2(22 2
= 2(2
Step: 11
Length of the minor axis = 2b
= 2(2) = 4 units
= 2(2) = 4 units
Step: 12
[Relation between a b c
Step: 13
Step: 14
[Take square root on both sides of the equation.]
Step: 15
So, the foci of the ellipse are (2, 0) and (- 2, 0).
[The foci of the ellipse are (c c
Step: 16
From the given graphs, we can observe that the ellipse in Graph 4 have center at the origin, foci as (2, 0) and (- 2, 0), length of the major axis as 42 x 2 y
Step: 17
Therefore, Graph 4 represents the given equation of the ellipse.
Correct Answer is : Graph 4
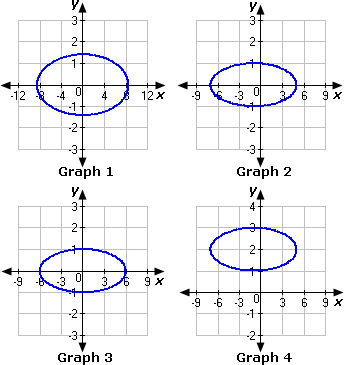
A. Graph 1
B. Graph 2
C. Graph 4
D. Graph 3
Step: 1
[Given.]
Step: 2
[Divide both sides of the equation by 36.]
Step: 3
The standard form of the equation of ellipse is ( x - h ) 2 a 2 ( y - k ) 2 b 2
[(x y h k
Step: 4
Compare the given equation with the standard form of the equation of ellipse.
Step: 5
The center of the ellipse is at (0, 0).
Step: 6
Step: 7
[Take square root on both sides of the equation.]
Step: 8
Step: 9
[Take square root on both sides of the equation.]
Step: 10
Length of the major axis = 2a
= 2(6) = 12 units
= 2(6) = 12 units
Step: 11
Length of the minor axis = 2b
= 2(1) = 2 units
= 2(1) = 2 units
Step: 12
[Relation between a b c
Step: 13
Step: 14
[Take square root on both sides of the equation.]
Step: 15
So, the foci of the ellipse are (3 5 3 5
[The foci of the ellipse are (c c
Step: 16
From the given graphs, we can observe that the ellipse in Graph 3 have center at the origin, foci as (3 5 3 5 x y
Step: 17
Therefore, Graph 3 represents the given equation of the ellipse.
Correct Answer is : Graph 3
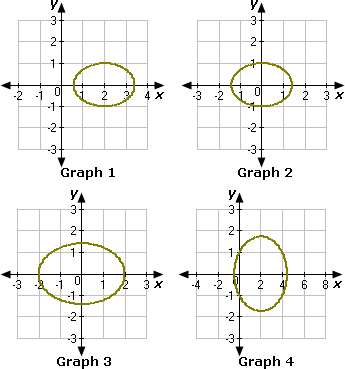
A. Graph 1
B. Graph 4
C. Graph 3
D. Graph 2
Step: 1
[Given.]
Step: 2
[Divide both sides of the equation by 2.]
Step: 3
The standard form of the equation of ellipse is ( x - h ) 2 a 2 ( y - k ) 2 b 2
[(x y h k
Step: 4
Compare the given equation with the standard form of the equation of ellipse.
Step: 5
The center of the ellipse is at (0, 0).
Step: 6
Step: 7
[Take square root on both sides of the equation.]
Step: 8
Step: 9
[Take square root on both sides of the equation.]
Step: 10
Length of the major axis = 2a
= 22
= 2
Step: 11
Length of the minor axis = 2b
= 2(1) = 2 units
= 2(1) = 2 units
Step: 12
[Relation between a b c
Step: 13
Step: 14
[Take square root on both sides of the equation.]
Step: 15
So, the foci of the ellipse are (1, 0) and (- 1, 0).
[The foci of the ellipse are (c c
Step: 16
From the given graphs, we can observe that the ellipse in Graph 2 have center at the origin, foci as (1, 0) and (- 1, 0), length of the major axis as 2rout(2) units and minor axis as 2 units, x 2 y
Step: 17
Therefore, Graph 2 represents the given equation of the ellipse.
Correct Answer is : Graph 2
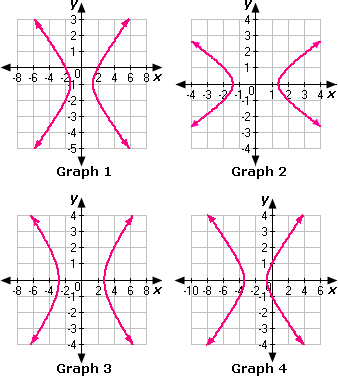
A. Graph 4
B. Graph 2
C. Graph 3
D. Graph 1
Step: 1
The standard form of the equation x 2 a 2 y 2 b 2
Step: 2
Compare x y
Step: 3
The center of this hyperbola is at the origin. According to the equation, a a 2 b b
The coordinates of the vertices are (2 2
The coordinates of the vertices are (
Step: 4
So, the hyperbola passes through the points (2 2
Step: 5
The points (0, - 1) and (0, 1) and the points (2 2
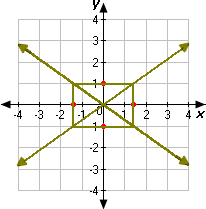

Step: 6
Now we can sketch the hyperbola. The graph goes through the points (2 2
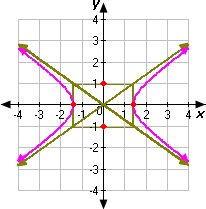

Step: 7
Therefore, Graph 2 represents the equation x y
Correct Answer is : Graph 2
A. Graph 4
B. Graph 1
C. Graph 2
D. Graph 3
Step: 1
The standard form of the equation x 2 a 2 y 2 b 2
Step: 2
Compare x 2 9 y 2 1 6
Step: 3
The center of this hyperbola is at the origin. According to the equation, a a b b
The coordinates of the vertices are (3, 0) and (- 3, 0).
The coordinates of the vertices are (3, 0) and (- 3, 0).
Step: 4
So, the hyperbola passes through the points (3, 0) and (- 3, 0).
Step: 5
The points (0, - 4) and (0, 4) and the points (3, 0) and (- 3, 0) can be used to form a rectangle whose diagonals are the asymptotes of the hyperbola.

Step: 6
Now we can sketch the hyperbola. The graph goes through the points (3, 0) and (- 3, 0) and get closer and closer to the asymptotes as we get farther and farther from the center of the figure.
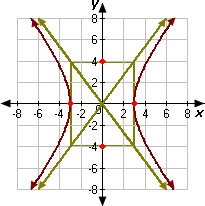

Step: 7
Therefore, Graph 3 represents the equation x 2 9 y 2 1 6
Correct Answer is : Graph 3
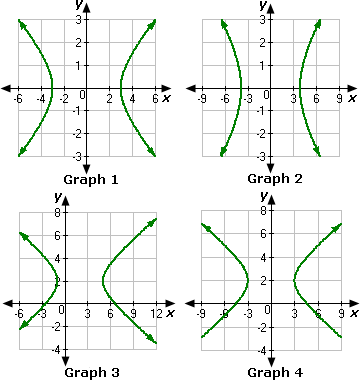
A. Graph 1
B. Graph 4
C. Graph 3
D. Graph 2
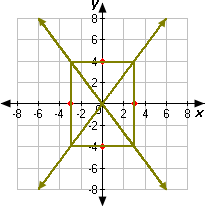
Step: 1
The standard form of the equation x 2 a 2 y 2 b 2
Step: 2
Compare 3x 2 y 2
Step: 3
The center of this hyperbola is at the origin. According to the equation, a a b b 3
The coordinates of the vertices are (3, 0) and (- 3, 0).
The coordinates of the vertices are (3, 0) and (- 3, 0).
Step: 4
So, the hyperbola passes through the points (3, 0) and (- 3, 0).
Step: 5
The points (0, - 3 3

Step: 6
Now we can sketch the hyperbola. The graph goes through the points (3, 0) and (- 3, 0) and get closer and closer to the asymptotes as we get farther and farther from the center of the figure.

Step: 7
Therefore, Graph 1 represents the equation 3x 2 y 2
Correct Answer is : Graph 1
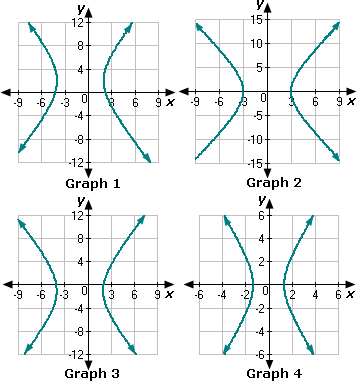
A. Graph 3
B. Graph 4
C. Graph 2
D. Graph 1
Step: 1
The standard form of the equation x 2 a 2 y 2 b 2
Step: 2
Compare 25x 2 y 2
Step: 3
The center of this hyperbola is at the origin. According to the equation, a a b b
The coordinates of the vertices are (3, 0) and (- 3, 0).
The coordinates of the vertices are (3, 0) and (- 3, 0).
Step: 4
So, the hyperbola passes through the points (3, 0) and (- 3, 0).
Step: 5
The points (0, - 5) and (0, 5) and the points (3, 0) and (- 3, 0) can be used to form a rectangle whose diagonals are the asymptotes of the hyperbola.
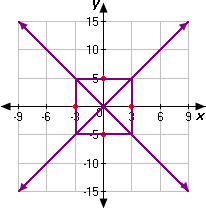

Step: 6
Now we can sketch the hyperbola. The graph goes through the points (3, 0) and (- 3, 0) and get closer and closer to the asymptotes as we get farther and farther from the center of the figure.
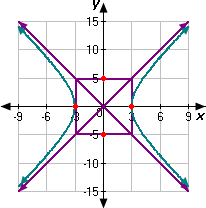

Step: 7
Therefore, Graph 2 represents the equation 25x 2 y 2
Correct Answer is : Graph 2
- Identifying and Using the Slopes of Parallel and Perpendicular Lines-Geometry-Solved Examples
- Writing Linear Equations of Parallel and Perpendicular Lines-Geometry-Solved Examples
- Equations of Circles-Geometry-Solved Examples
- Standard Forms and Equations of Ellipses and Parabolas-Geometry-Solved Examples
- Identifying Conic Sections-Geometry-Solved Examples
Related Worksheet
- Conic Section