Solved Examples and Worksheet for Solving Quadratic Linear Systems of Equations

Q1Solve the system:
4x + y = 12
x2 = 8x + y

A. (6, -12) and (- 2, 20)
B. (0, 0) and (- 2, - 20)
C. (6, - 2) and (-12, 20)
D. (6, -12) and (- 2, - 20)

Solutions
Share 
Step: 1
The system contains the equation of a line and a parabola. The maximum number of points of intersection is two. So, there are at most two solutions.
Step: 2
4x + y = 12
  [Equation of line.]
Step: 3
y = 12 - 4x
  [Solve for y.]
Step: 4
x2 = 8x + y
  [Equation of parabola.]
Step: 5
x2 = 8x + (12 - 4x)
  [Replace y with 12 - 4x.]
Step: 6
x2 - 4x - 12 = 0
  [Simplify.]
Step: 7
(x - 6)(x + 2) = 0
  [Factor.]
Step: 8
x = 6 or x = - 2
  [Solve for x.]
Step: 9
At x = 6, y = 12 - 4(6) = -12
  [Simplify.]
Step: 10
At x = - 2, y = 12 - 4(- 2) = 20
  [Simplify.]
Step: 11
The points of intersection are (6, -12) and (- 2, 20).
Correct Answer is :   (6, -12) and (- 2, 20)
Q2Solve the system:
x2 + y2 = 128
x = y

A. (8, - 8), (- 8, - 8)
B. (8, 8), (8, - 8)
C. (8, - 8), (- 8, 8)
D. (8, 8), (- 8, - 8)

Solutions
Share 
Step: 1
The system contains the equation of a line and a circle. The maximum number of points of intersection is 2. Therefore, there are at most 2 solutions.
Step: 2
y = x
  [Equation of line.]
Step: 3
x2 + y2 = 128
  [Equation of circle.]
Step: 4
x2 + x2 = 128
  [Replace y with x.]
Step: 5
2x2 = 128
  [Simplify.]
Step: 6
x = 8 or x = - 8
  [Solve for x.]
Step: 7
At x = 8, y = 8
  [Use the equation y = x.]
Step: 8
At x = - 8, y = - 8
  [Use the equation y = x.]
Step: 9
The points of intersection (or) the solutions are (8, 8), (- 8, - 8).
Correct Answer is :   (8, 8), (- 8, - 8)
Q3Find the solutions of the quadratic linear system:
y = x + 1
y = x2 - 78x + 1561
A. (39, 40) and (40, 41)
B. (40, 39) and (41, 40)
C. (39, 41) and (40, 40)
D. (40, 40) and (39, 41)

Solutions
Share 
Step: 1
y = x + 1 ..............(1)
Step: 2
y = x2 - 78x + 1561 .........(2)
Step: 3
x + 1 = x2 - 78x + 1561
  [Substitute the value of y of equation 1 in equation 2.]
Step: 4
x2 - 79x + 1560 = 0
  [Simplify.]
Step: 5
(x - 39)(x - 40) = 0
  [Factor.]
Step: 6
x = 39, 40
Step: 7
At x = 39, y = 39 + 1 = 40
  [Use equation 1.]
Step: 8
At x =40, y = 40 + 1 = 41
  [Use equation 1.]
Step: 9
So, the solutions of the quadratic linear system are (39, 40) and (40, 41).
Correct Answer is :   (39, 40) and (40, 41)
Q4Find the solutions of the quadratic linear system:
y = 4x - 6
y = x2 - 9x + 30
A. (- 9, - 42) and (- 4, - 22)
B. (9, 36) and (4, 16)
C. (10, 31) and (5, 11)
D. (9, 30) and (4, 10)

Solutions
Share 
Step: 1
y = 4x - 6 ..............(1)
Step: 2
y = x2 - 9x + 30 .........(2)
Step: 3
4x - 6 = x2 - 9x + 30
  [Substitute the the value of y of equation 1 in equation 2.]
Step: 4
x2 - 13x + 36 = 0
  [Simplify.]
Step: 5
(x - 9)(x - 4) = 0
  [Factor.]
Step: 6
x = 9, 4
Step: 7
At x = 9, y = 4(9) - 6 = 30
  [Use equation 1.]
Step: 8
At x = 4, y = 4(4) - 6 = 10
  [Use equation 1.]
Step: 9
So, the solutions of the quadratic linear system are (9, 30) and (4, 10).
Correct Answer is :   (9, 30) and (4, 10)
Q5Find the solutions of the quadratic linear system:
y = x + 1
y = x2 - 28x + 211

A. (13, 14) and (14, 15)
B. ( 14, 13) and (- 15, - 14)
C. (14, 15) and (15, 16)
D. (- 15, - 14) and (- 14, - 13)

Solutions
Share 
Step: 1
y = x + 1 ..............(1)
Step: 2
y = x2 - 28x + 211 .........(2)
Step: 3
x + 1 = x2 - 28x + 211
  [Substitute the value of y of equation 1 in equation 2.]
Step: 4
x2 - 29x + 210 = 0
  [Simplify.]
Step: 5
(x - 14)(x - 15) = 0
  [Factor.]
Step: 6
x = 14, 15
Step: 7
At x = 14, y = 14 + 1 = 15
  [Use equation 1.]
Step: 8
At x = 15, y = 15 + 1 = 16
  [Use equation 1.]
Step: 9
So, the solutions of the quadratic linear system are (14, 15) and (15, 16).
Correct Answer is :   (14, 15) and (15, 16)
Q6Solve the system:
x2 + y2 = 50
x = y

A. (5, - 5), (- 5, - 5)
B. (5, 5), (- 5, - 5)
C. (5, - 5), (- 5, 5)
D. (5, 5), (5, - 5)

Solutions
Share 
Step: 1
The system contains the equation of a line and a circle. The maximum number of points of intersection is 2. Therefore, there are at most 2 solutions.
Step: 2
y = x
  [Equation of line.]
Step: 3
x2 + y2 = 50
  [Equation of circle.]
Step: 4
x2 + x2 = 50
  [Replace y with x.]
Step: 5
2x2 = 50
  [Simplify.]
Step: 6
x = 5 or x = - 5
  [Solve for x.]
Step: 7
At x = 5, y = 5
  [Use the equation y = x.]
Step: 8
At x = - 5, y = - 5
  [Use the equation y = x.]
Step: 9
The points of intersection (or) the solutions are (5, 5), (- 5, - 5).
Correct Answer is :   (5, 5), (- 5, - 5)
Q7Solve the system:
x2 + 2y2 = 12
y = x
A. (2, - 2), (- 2, - 2)
B. (2, 2), (2, - 2)
C. (2, 2), (- 2, - 2)
D. (2, 2), (- 2, 2)

Solutions
Share 
Step: 1
The system contains the equation of a line and an ellipse. The maximum number of points of intersection is two, and therefore atmost number of solutions are two.
Step: 2
y = x
  [Equation of line.]
Step: 3
x2 + 2y2 = 12
  [Equation of ellipse.]
Step: 4
x2 + 2x2 = 12
  [Replace y with x.]
Step: 5
x2 = 4
  [Simplify.]
Step: 6
x = 2 or x = - 2
  [Solve for x.]
Step: 7
At x = 2, y = 2
  [Use the equation y = x.]
Step: 8
At x = - 2, y = - 2
  [Use the equation y = x.]
Step: 9
The points of intersection or solutions are (2, 2), (- 2, - 2).
Correct Answer is :   (2, 2), (- 2, - 2)
Q8Solve the system algebraically: y = 4x2 and 7x + y = -3.
A. (-14, 94) and (1, -4)
B. (- 34, 94) and (-1, 4)
C. (-34, 4) and (-1, 4)
D. (-94, 34) and (-1, 4)

Solutions
Share 
Step: 1
y = 4x2, 7x + y = -3
Step: 2
7x + 4x2 = -3
  [Substitute y = 4x2 in 7x + y = -3.]
Step: 3
4x2 + 7x + 3 = 0
Step: 4
(4x + 3)(x + 1)= 0
  [Factor.]
Step: 5
x = -34, -1
  [Solve for x.]
Step: 6
y = 94, 4
  [substitute x values in y = 4x2.]
Step: 7
The system of equations has two solutions (- 34, 94) and (-1, 4).
Correct Answer is :   (- 34, 94) and (-1, 4)
Q9Solve the system y = x2 + 3x and x + y = 5 algebraically.

A. (-5, 10) and (1, 4)
B. (1, -4) and (-5, 10)
C. (-10, 4) and (1, 5)
D. (1,-5) and (-4, 10)

Solutions
Share 
Step: 1
y = x2 + 3x, x + y = 5
Step: 2
x2 + 3x + x = 5
  [Substitute y = x2 +3x in x + y = 5.]
Step: 3
x2 + 4x - 5 = 0
Step: 4
(x + 5)(x - 1)= 0
  [Factor.]
Step: 5
x = -5, 1
  [Solve for x.]
Step: 6
At x = -5, (-5) + y = 5
  [ Use equation 2.]
Step: 7
y = 10
Step: 8
At x = 1, (1) + y = 5
  [ Use equation 2.]
Step: 9
y = 4
Step: 10
The system of equations has two solutions (-5, 10) and (1, 4).
Correct Answer is :   (-5, 10) and (1, 4)
Q10Solve the quadratic linear system by graphing the equations:
y = x2 - 3x + 1
y=2x - 5

A. (-2, 1) and (3, 1)
B. (2, 3) and (3, -3)
C. (2, -1) and (3, 1)
D. (2, 2) and (3, -3)

Solutions
Share 
Step: 1
y = x2-3x + 1.........................(1)
Step: 2
y = 2x - 5..............................(2)
Step: 3
  [Graph the equations 1 and 2.]

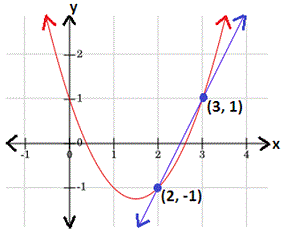
Step: 4
From the graph, the solutions of the quadratic linear system are (2, -1) and (3, 1)
Correct Answer is :   (2, -1) and (3, 1)
Q11Find the solutions of the quadratic linear system:
y = x2 + x - 2
y= - x + 1
A. (1, 0) and (-3, 4)
B. (1, 2) and (3, 4)
C. (1, 0) and (-3, 4)
D. (-1, 0) and (-3, 4)

Solutions
Share 
Step: 1
y = x2 + x - 2.........................(1)
Step: 2
y = - x + 1..................................(2)
Step: 3
x2 + x - 2 = - x + 1
  [Equate the values of y, from both the equations.]
Step: 4
x2 + 2x - 3 = 0
  [Simplify.]
Step: 5
(x - 1)(x + 3) = 0
  [Factor.]
Step: 6
x = 1, - 3
  [Solve for x.]
Step: 7
At x = 1, y = - (1) +1 = 0
  [ Use equation 2.]
Step: 8
At x = - 3, y = - (- 3) + 1 = 4
  [ Use equation 2.]
Step: 9
So, the solutions of the quadratic linear system are (1, 0) and (-3, 4).
Correct Answer is :   (1, 0) and (-3, 4)
Q12Solve the quadratic linear system by graphing the equations:
y = 1.5x - 2.7
y = x2 - 3.5x + 1.3
A. (1, -0.2) and (6, 1.3)
B. (1, 1.2) and (4, -3.3)
C. (1, 1.2) and (4, 0.3)
D. (1, -1.2) and (4, 3.3)

Solutions
Share 
Step: 1
y = 1.5x - 2.7 .........................(1)
Step: 2
y = x2 - 3.5x + 1.3....................(2)
Step: 3
  [Graph the equations 1 and 2.]

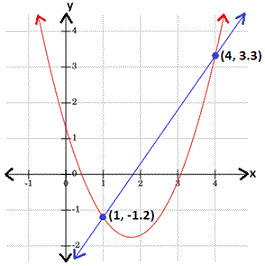
Step: 4
From the graph, the solutions of the quadratic linear system are (4, 3.3) and (1, -1.2).
Correct Answer is :   (1, -1.2) and (4, 3.3)

HighSchool Math