ISOMETRY

Definition Of Isometry

An isometry is a transformation in which the original figure and its image are congruent.

More About Isometry

Isometry is invariant with respect to distance. That is, in an isometry, the distance between any two points in the original figure is the same as the distance between their corresponding images in the transformed figure (image).
Reflections, rotations, translations are isometries.
Dilation is not an isometry.

Video Examples: Regular and Isometry

Example of Isometry

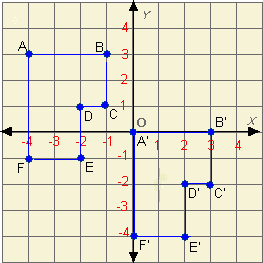
The figure shows a translation, an isometry. 
An irregular polygon ABCDE is translated to A'B'C'D'E'.
Notice that the distance between A and B is the same as the distance between their image A' and B'.

Solved Example on Isometry

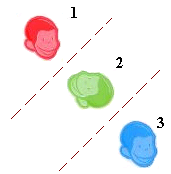
Ques: What isometry maps figure 1 to figure 3? 

Choices:

A. reflection 
B. translation 
C. rotation 
D. none of these 
Correct Answer: B

Solution:

Step 1: An isometry is a transformation in which the original figure and its image are congruent.
Step 2: A reflection flips the figure across a line. The new figure is a mirror image of the original figure.
Step 3: Figure 2 is a reflection of Figure 1 and Figure 3 is a reflection of Figure 2. 
Step 4: A translation is the composition of two reflections in parallel lines.
Step 5: So, the isometry that maps Figure 1 to Figure 3 is a translation.