Directrix
Definition Of Directrix Of A Conic Section
Directrix of a conic section is a line such that ratio of the distance of the points on the conic section from focus to its distance from directrix is constant.
More About Directrix of a Conic Section
If the ratio (r) of the distance of any point on the conic section from focus to its distance from directrix is equal to 1, then the conic section is a parabola. If it is less than 1, then it is ellipse; and if it is greater than 1, then the conic section is a hyperbola
Example Of Directrix Of A Conic Section
The given figure represents the directrix of Ellipse, Parabola, and Hyperbola
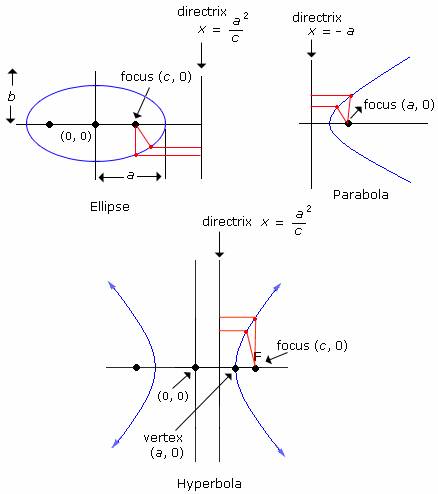
The directrixes of three different conic sections, 'Ellipse', 'Parabola', and 'Hyperbola' are shown above.
Video Examples: Parabola Focus and Directrix 1
Solved Example on Directrix of a Conic Section
Ques: Find the equation of directrix of the parabola y2 = 12x.
Choices:
A. y = - 3
B. x= 3
C. x = - 3
D. y = 3
E. X = 12
Correct Answer: C
Solution:
Step 1: y2= 12x [Write the equation of the parabola.]
Step 2: 4 P = 12, so P = 3 [Compare with y2 = 4Px.]
Step 3: So, x = - 3 is the equation of the directrix of the parabola. [The equation of the directrix of the parabola y2 = 4Px is x = - p.]