Solved Examples and Worksheet for Measures of Inscribed Angles

Q1In the given figure, O is the center of the circle. What is m∠QPR, if m∠OQR = 22°?


A. 79
B. 11
C. 136
D. 68

Solutions
Share 
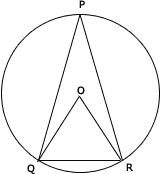
Step: 1
Given, ∠OQR = 22o.
Step: 2
⇒ ∠QOR = 180o - (2 × 22o) = 136o.
Step: 3
The angle made by the chord QR at the center of the circle is twice the angle made by it at any point on the circle.
Step: 4
So, m ∠QPR = 136/2 = 68°.
Correct Answer is :   68
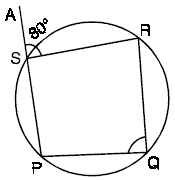
Q2In the figure shown, PQRS is a quadrilateral inscribed in a circle. Side PS is extended to the point A. Which of the following statements are true, if ∠ASR = 80°?


A. ∠R = 80°
B. ∠Q = 80°
C. ∠P = 80°
D. ∠PSR = 80°

Solutions
Share 
Step: 1
Quadrilateral PQRS is a cyclic quadrilateral.
Step: 2
Therefore,∠ASR = ∠PQR
Step: 3
From the given choices, ∠Q=80°
Correct Answer is :   ∠Q = 80°
Q3Find the value of m∠BOC in the figure shown.


A. 68°
B. 108°
C. 100°
D. 122°

Solutions
Share 
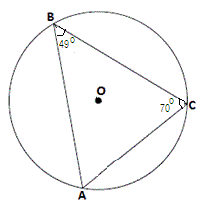
Step: 1
m∠ ABC + m∠ACB + m∠ BAC = 180°
  [Sum of the angles in a triangle is 180°.]
Step: 2
49° + 70° + m∠BAC = 180°
Step: 3
m∠ BAC = 180° - 119° = 61°
Step: 4
Join BO and CO.
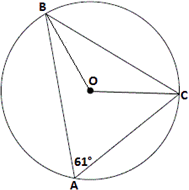
Step: 5
m∠BOC = 2 × m∠BAC = 2 × 61° = 122°
  [Inscribed angle theorem.]
Step: 6
Therefore, m∠ BOC = 122° .
Correct Answer is :   122°
Q4Find ∠AOC in the figure shown.


A. 51°
B. 67°
C. 82°
D. 78°

Solutions
Share 
Step: 1
m∠ ABC = 39°
  [Given.]
Step: 2
m∠AOC = 2 × m∠ABC
  [Inscribed angle theorem.]
Step: 3
= 2 × 39° = 78°
  [Substitute.]
Step: 4
Therefore, m∠ AOC = 78°.
Correct Answer is :   78°
Q5In the figure shown, if O is the center of the circle, then x equals ______.


A. 38
B. 52
C. 32
D. 104

Solutions
Share 
Step: 1
m∠ AOB = 76°
  [Given.]
Step: 2
m∠ ACB = 12 × m∠ AOB
  [Inscribed angle theorem.]
Step: 3
x° = 12 × 76° = 38°
  [Substitute.]
Step: 4
Therefore, x = 38.
Correct Answer is :   38
Q6In the figure shown, if O is the center of the circle and m∠BOC = 74°, then find the measure of x.

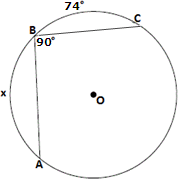
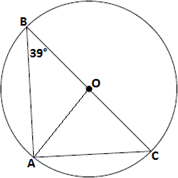
A. 98°
B. 106°
C. 94°
D. 86°

Solutions
Share 
Step: 1
m∠BOC = 74° and m∠ABC = 90°
  [Given.]
Step: 2
Join AC and BO.
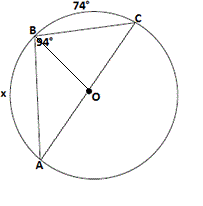
Step: 3
m∠BAC = 12 × m∠BOC = 12 × 74° = 37°
  [Inscribed angle theorem.]
Step: 4
m∠ABC + m∠ACB + m∠BAC = 180°
  [Sum of the angles in a triangle is 180°.]
Step: 5
90° + m∠ACB + 37° = 180°
Step: 6
m∠ACB = 180° - 127° = 53°
Step: 7
m∠AOB = 2 × m∠ACB
  [Inscribed angle theorem.]
Step: 8
x = 2 × 53° = 106°
  [Substitute.]
Step: 9
Therefore, x = 106°.
Correct Answer is :   106°
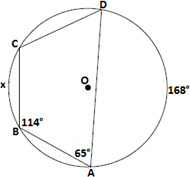
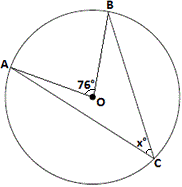
Q7In the figure shown, if O is the center of the circle and m∠AOD = 168°, then find the measure of x.


A. 60°
B. 80°
C. 70°
D. 65°

Solutions
Share 
Step: 1
m∠AOD = 168°, m∠ABC = 114° and m∠ BAD = 65°
  [Given.]
Step: 2
Join BD.
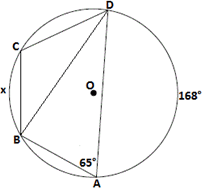
Step: 3
m∠ABD = 12× m∠AOD = 12× 168° = 84°
  [Inscribed angle theorem.]
Step: 4
m∠ ABC = m∠ ABD + m∠ CBD
  [Angle Addition Postulate.]
Step: 5
114° = 84° + m∠ CBD
  [Substitute.]
Step: 6
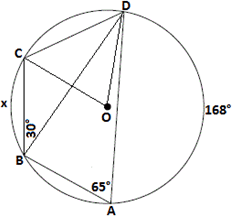
m∠ CBD = 114° - 84° = 30°
Step: 7
Also, m∠ABD + m∠ADB + m∠BAD = 180°
  [Sum of the angles in a triangle is 180°.]
Step: 8
84° + m∠ADB + 65° = 180°
Step: 9
m∠ADB = 180° - 149° = 31°
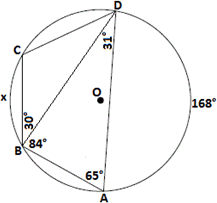
Step: 10
Join AO and BO.
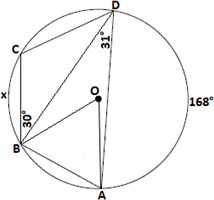
Step: 11
m∠AOB = 2 × m∠ADB = 2 × 31° = 62°
  [Inscribed angle theorem.]
Step: 12
Join CO and DO.
Step: 13
m∠COD = 2 × m∠CBD = 2 × 30° = 60°
  [Inscribed angle theorem.]
Step: 14
Now, m∠AOD + m∠AOB + m∠BOC + m∠COD = 360°
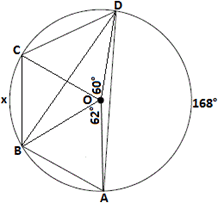
  [The sum of angles around a point will always be 360°.]

Step: 15
168° + 62° + x + 60° = 360°
  [Substitute.]
Step: 16
So, x = 360° - 290° = 70°
Correct Answer is :   70°
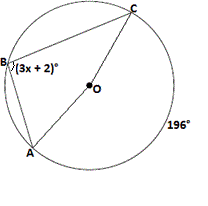
Q8In the figure shown, if O is the center of the circle, then x equals ______.

A. 33
B. 31
C. 38
D. 32

Solutions
Share 
Step: 1
m∠ ABC = 12× (Reflex ∠ AOC)
  [Inscribed angle theorem.]
Step: 2
(3x + 2)° = 12 × 196° = 98°
  [Substitute.]
Step: 3
3x = 98 - 2 = 96
Step: 4
Therefore, x = 963 = 32.
Correct Answer is :   32
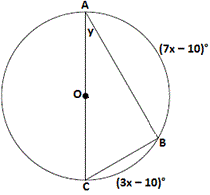
Q9In the figure shown, if O is the center of the circle, then y equals ______.

A. 25°
B. 35°
C. 32°
D. 30°

Solutions
Share 
Step: 1
Join BO.
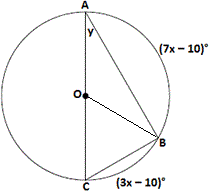
Step: 2
m∠ AOB = (7x - 10)° and m∠BOC = (3x - 10)°
   [Given]
Step: 3
m∠ AOB + m∠BOC = 180°
  [Linear pair.]
Step: 4
(7x - 10)° + (3x - 10)° = 180°
  [Substitute.]
Step: 5
10x - 20 = 180
Step: 6
10x = 200 ⇒ x = 20010 = 20
Step: 7
m∠ BOC = (3x - 10)° = (3(20) - 10)° = 50°
Step: 8
y = 12 × 50° = 25°
  [Inscribed angle theorem.]
Correct Answer is :   25°
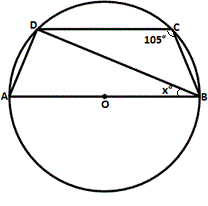
Q10In the figure shown, if O is the center of the circle, then x equals ______.

A. 15
B. 45
C. 30
D. 25

Solutions
Share 
Step: 1
m∠ BCD = 105°
  [Given]
Step: 2
The opposite angles of a quadrilateral inscribed in a circle are supplementary.
Step: 3
m∠DAB = 180° - m∠ BCD
  [ABCD is a cyclic quadrilateral.]
Step: 4
m∠DAB = 180° - 105° = 75°
  [Substitute and simplify.]
Step: 5
m∠ADB = 90°
  [Angle in a semi circle.]
Step: 6
In ∠ADB, m∠ DAB + m∠ ABD + m∠ADB = 180°
  [Triangle Angle- Sum Theorem.]
Step: 7
m∠ ABD = 180° - (m∠ DAB + m∠ADB)
Step: 8
x° = 180° - (75° + 90°) = 180° - 165° = 15°
  [Substitute and simplify.]
Step: 9
Therefore, x = 15.
Correct Answer is :   15
    Related Worksheet

HighSchool Math