Fitting Exponential Models to Data-Algebra1-Solved Examples

Solved Examples and Worksheet for Fitting Exponential Models to Data

Q1Number of employees in an organization are shown in the table, where t represents time in years since 1991. Find the exponential model for the data.

Years since 1991(t)	0	1	2	3	4
Number of employees	200	300	450	675	1012

A. R = 200(2.5)^t
B. R = 300(0.75)^t
C. R = 300(1.5)^t
D. R = 200(1.5)^t

Solutions

Step: 1

Let the exponential function be R = M(N)^t.

Step: 2

For t = 0, R = 200

Step: 3

200 = M(N)⁰

Step: 4

M = 200

Step: 5

For t = 1, R = 300 ⇒ 300 = 200N

Step: 6

N = 1.5

Step: 7

So, the exponential function that best fits the data is R = 200(1.5)^t.

Correct Answer is : R = 200(1.5)^t

Q2Choose the exponential model for the data shown.

x	0	1	2	3	4
f(x)	5	20	80	320	1280

A. f(x) = 5 · (45)^x
B. f(x) = 5 · 4^x
C. f(x) = 4 · 5^x
D. f(x) = 5 · 4x

Solutions

Q3Choose an exponential function for the table of values.

x	y
-3	10
-2	100
-1	1000
0	10000
1	100000

A. y = 10000 · x¹⁰
B. y = 10000^{(x + 1)}
C. y = 10000 · 10^x
D. y = 10000 · 10^{- x}

Solutions

Step: 1

The table of values obtained by substituting x = -3, -2, -1, 0, 1 in the exponential function y = 10000 · 10^x.

Correct Answer is : y = 10000 · 10^x

Q4Choose the exponential model for the data shown.

x	- 2	- 1	0	1	2
f(x)	89	43	2	3	92

A. f(x) = 2 · (32)^x
B. f(x) = 2 · 3^x
C. f(x) = 2 · 5^x
D. f(x) = 2

Solutions

Step: 1

Let the exponential function be f(x) = M (N)^x.

Step: 2

At x = 0, f(x) = 2

[From the table.]

Step: 3

2 = M (N)⁰ ⇒ M = 2

[Substitute the values in the exponential function given in step 1.]

Step: 4

At x = 1, f(x) = 3

[From the table.]

Step: 5

3 = M (N)¹

[Substitute the values in the exponential function given in step 1.]

Step: 6

3 = 2N ⇒ N = 32

[Substitute M = 2.]

Step: 7

Hence, the exponential function is f(x) = 2 · (32)^x.

[Substitute the values of M & N in the exponential function given in step 1.]

Correct Answer is : f(x) = 2 · (32)^x

Q5George bought a house for $48000 in the year 2005. The following table shows the house value for the subsequent years. Choose the exponential model for the data shown.

Years since 2005(t)	0	1	2	3	4
value ($y)	55000	62150	70229.5	79359.33	89676.04

A. y = 55000(1.21)^t
B. y = 55000(1.25)^t
C. y = 55000(1.13)^t
D. y = 55000(1.31)^t

Solutions

Step: 1

Let the exponential function be y = M(N)^t.

Step: 2

At t = 0, y = 55000

[From the table.]

Step: 3

55000 = M(N)⁰

Step: 4

M = 55000

Step: 5

At, t = 1, y = 62150

Step: 6

62150 = 55000N

Step: 7

N = 1.13

[Simplify.]

Step: 8

So, the exponential function that best fits the data is y = 55000(1.13)^t

[Substitute the values of M & N in the exponential function given in step 1.]

Correct Answer is : y = 55000(1.13)^t

Q6Profits of a company are shown in the table, where t represents time in years since 2006. Find the exponential model for the data.

Yrs from 2006 (t)	0	1	2	3	4
Profit billion$ (P)	9	12.15	16.40	22.14	29.89

A. P = - 9(1.35 )^t
B. P = 16.40(1.49)^t
C. P = - 12.15(1.49) ^t
D. P = 9(1.35)^t

Solutions

Step: 1

Let the exponential function be P = M(N)^t.

Step: 2

For t = 0, P = 9

Step: 3

9 = M(N)⁰

Step: 4

M = 9

Step: 5

For t = 1, P = 12.15

Step: 6

12.15 = 9N

[from step 4.]

Step: 7

N = 1.35

[Simplify.]

Step: 8

So, the exponential function that best fits the data is P = 9(1.35)^t

[Substitute the values of P, M and N in step 1.]

Correct Answer is : P = 9(1.35)^t

Q7Choose the exponential model for the data shown.

A. f(x) = 32(- 2)^x
B. f(x) = 16( - 4)^x
C. f(x) = 32(2)^x
D. f(x) = 16(4)^x

Solutions

Step: 1

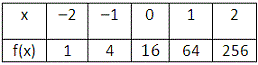
Let the exponential function be f(x) = M(N)^x

Step: 2

At x = 0, f(x) = 16

[From the table.]

Step: 3

16 = M(N)⁰ ⇒ M = 16

[Substitute the values in the exponential function given in step 1.]

Step: 4

At x = 1, f(x) = 64.

[From the table.]

Step: 5

64 = M(N)¹

[Substitute the values in the exponential function given in step 1.]

Step: 6

16N = 64 ⇒ N = 6416 = 4

[Substitute M = 16.]

Step: 7

Hence, the exponential function is f(x) = 16(4)^x

[Substitute the values of M & N in the exponential function given in step 1.]

Correct Answer is : f(x) = 16(4)^x

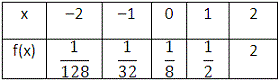
Q8Choose the exponential model for the data shown.

A. f(x) = 18(8)^x
B. f(x) = 14(8)^x
C. f(x) = 18(2)^x
D. f(x) = 18(4)^x

Solutions

Step: 1

Let the exponential function be f(x) = M(N)^x

Step: 2

At x = 0, f(x) = 18.

[From the table.]

Step: 3

18 = M(N)⁰ ⇒ M = 18

[Substitute the values in the exponential function given in step 1.]

Step: 4

At x = 1, f(x) = 12

[From the table.]

Step: 5

12 = M(N)¹

[Substitute the values in the exponential function given in step 1.]

Step: 6

18N = 12 ⇒ N = 82 = 4

[Substitute M = 18.]

Step: 7

Hence, the exponential function is f(x) = 18(4)^x

[Substitute the values of M & N in the exponential function given in step 1.]

Correct Answer is : f(x) = 18(4)^x

Q9Revenues of a factory are shown in the table, where t represents time in years since 2006. Find the exponential model for the data.

A. R = 4(1.5)^t
B. R = 4(0.75)^2t
C. R = 4(1.25)^t
D. R = 4(1.05)^t

Solutions

Step: 1

Let the exponential function be R = M(N)^t

Step: 2

At t = 0, R = 4.

[From the table.]

Step: 3

4 = M(N)⁰ ⇒ M = 4

[Substitute the values in the exponential function given in step 1.]

Step: 4

At t = 1, R = 6.

[From the table.]

Step: 5

6 = M(N)¹

[Substitute the values in the exponential function given in step 1.]

Step: 6

4N = 6 ⇒ N = 64 = 1.5

[Substitute M = 4.]

Step: 7

Hence, the exponential function is R = 4(1.5)^t

[Substitute the values of M & N in the exponential function given in step 1.]

Correct Answer is : R = 4(1.5)^t

Solved Examples and Worksheet for Fitting Exponential Models to Data

Related Worksheet

Related Topic

HighSchool Math