Solved Examples and Worksheet for Pythagorean Theorem

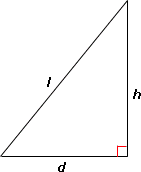
Q1One end of a wire with a length of 20 feet is tied to the top of the pole and the other end is fixed on the ground at a distance of 12 feet from the foot of the pole. What is the height of the pole?

A. 48 feet
B. 16 feet
C. 28 feet
D. 36 feet

Solutions
Share 
Step: 1
d2 + h2 = l2
  [Apply Pythagorean theorem.]
Step: 2
h2 = l2 - d2
  [Subtract d2 from both sides.]
Step: 3
h2 = 202 - 122
  [Substitute l and d.]
Step: 4
= 400 - 144
  [Apply exponents and simplify.]
Step: 5
= 256
  
Step: 6
⇒ h = 256
  [Take square root of both sides.]
Step: 7
= 16
  
Step: 8
Therefore, the height of the pole is 16 feet.
Correct Answer is :   16 feet
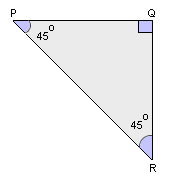
Q2The length of PR in the figure is 9√2 inches. What are the lengths of PQ and QR?


A. 9 inches and 9 inches
B. 6 inches and 4 inches
C. 4 inches and 4 inches
D. 2 inches and 3 inches

Solutions
Share 
Step: 1
The triangle is a 45o-45o-90o triangle.
Step: 2
Length of PR = 9√2 inches.
Step: 3
In a 45o- 45o-90o triangle, length of hypotenuse is √2 times the length of leg.
Step: 4
In ΔPQR, PQ and QR are congruent legs and PR is the hypotenuse.
Step: 5
PR = PQ√2
Step: 6
PQ = PR/√2
  [Divide each side by √2.]
Step: 7
PQ = 9√2/√2
  [Replace PR with 9√2.]
Step: 8
PQ = 9 inches
  [Simplify.]
Step: 9
Since the lengths of two legs are equal in 45o-45o-90o triangle, PQ = QR = 9 inches.
Step: 10
The lengths of PQ and QR are 9 inches and 9 inches.
Correct Answer is :   9 inches and 9 inches
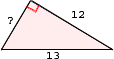
Q3What is the length of the third side of the triangle in the figure?


A. 5 units
B. 12 units
C. 8 units
D. 10 units

Solutions
Share 
Step: 1
If one angle of the triangle is 90°, then the triangle is a right triangle.
Step: 2
The side opposite to right angle is hypotenuse.
Step: 3
Let x be the length of the third side of the triangle.
Step: 4
According to Pythagorean theorem, in a right triangle, square of the hypotenuse = sum of the squares of other two sides.
Step: 5
Applying Pythagorean theorem, 132 = 122 + x2
Step: 6
169 = 144 + x2
  
Step: 7
169 - 144 = x2
  [Subtract 144 from both the sides.]
Step: 8
25 = x2
  
Step: 9
√25 = x
5 = x
  
Step: 10
The length of the third side of the triangle is 5 units.
Correct Answer is :   5 units
Q4Justin walked diagonally across a square garden of side 12 ft from one corner to the opposite corner. How far did he walk?

A. 17.09 ft
B. 18.09 ft
C. 15.85 ft
D. 16.97 ft

Solutions
Share 
Step: 1
Let s be the side of the square garden and d be the distance Justin walked.
Step: 2
All the angles of a square are right angles. So, the diagonal of the square will be the hypotenuse of the right triangle formed by two adjacent sides and the diagonal.
Step: 3
d2 = s2 + s2
  [Apply Pythagorean theorem.]
Step: 4
d2 = 122 + 122
  [Substitute s = 16.]
Step: 5
d2 = 144 + 144 = 288
  [Apply exponents and simplify.]
Step: 6
d = √288 = 16.97
  [Take square root on both sides.]
Step: 7
The total distance Justin walked is 16.97 ft.
Correct Answer is :   16.97 ft
Q5Find the value of a from the figure.


A. 12
B. 13
C. 16
D. 8

Solutions
Share 
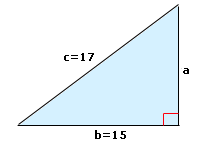
Step: 1
From the figure, c = 17 and b = 15
Step: 2
a2 + b2 = c2
  [Write Pythagorean theorem.]
Step: 3
a2 = c2 - b2
  [Subtract b2 from both sides.]
Step: 4
a2 = 172 - 152
  [Substitute for b and c.]
Step: 5
a2 = 289 - 225 = 64
  [Apply exponents and simplify.]
Step: 6
a = 64 = 8
  [Take square root of both sides.]
Step: 7
The value of a is 8.
Correct Answer is :   8
Q6A ladder which is 10 feet long is placed on a wall such that the top of the ladder touches the top of the wall. The bottom of the ladder is 6 feet away from the wall. What is the height of the wall?
A. 11 feet
B. 5 feet
C. 8 feet
D. 14 feet

Solutions
Share 
Step: 1
The length of the ladder l = 10 feet.
Step: 2
The distance from the foot of the ladder to the wall, d = 6 feet.
Step: 3
Let h be the height of the wall.
Step: 4
d2 + h2 = l2
  [Write Pythagorean theorem.]
Step: 5
h2 = l2 - d2
  [Subtract d2 from both sides.]
Step: 6
= 102 - 62
  [Substitute l and h.]
Step: 7
= 100 - 36
  [Apply exponents and simplify.]
Step: 8
= 64
  
Step: 9
h = √64
  [Take square root of both sides.]
Step: 10
= 8
  
Step: 11
Height of the wall = 8 feet.
Correct Answer is :   8 feet
Q7The lengths of the hypotenuse and the shorter leg of a right triangle are in the ratio 5:3 and the perimeter of the triangle is 60 inches. Find the length of the longer leg.

A. 25 inches
B. 20 inches
C. 15 inches
D. None of the above

Solutions
Share 
Step: 1
The lengths of hypotenuse and shorter leg of a right triangle are in the ratio 5:3
Step: 2
Let the length of hypotenuse and shorter leg be 5k and 3k respectively.
Step: 3
Let the length of longer leg be x.
Step: 4
x2 = (5k)2 - (3k)2
  [Apply Pythagorean theorem.]
Step: 5
x2 = 25k2 - 9k2
  [Evaluate powers.]
Step: 6
x = √(16k)2 = 4k
  [Subtract and find the positive square root.]
Step: 7
The perimeter of triangle = 60 inches.
Step: 8
Perimeter of the right triangle = 5k + 4k + 3k = 12k.
Step: 9
12k = 60
  
Step: 10
k = 6012= 5
  [Divide both sides with 12 and simplify.]
Step: 11
The length of longer leg = 4k = 4 x 5 = 20 inches.
Correct Answer is :   20 inches
Q8Pythagorean Theorem is applicable for _____.

A. right triangles only
B. any triangle
C. obtuse triangles only
D. None of the above

Solutions
Share 
Step: 1
Pythagorean Theorem is applicable only for right triangles.
Correct Answer is :   right triangles only
Q9If one side of a right triangle is 3 ft and the length of its hypotenuse is 4 ft, then find the length of the other side.
A. 5
B. 7 ft
C. 6 ft
D. 7 ft

Solutions
Share 
Step: 1
Let a be the length of the side and c be the length of hypotenuse.
Step: 2
Then, a = 3 ft and c = 4 ft.
Step: 3
Let b be the length of the side to be calculated.
Step: 4
According to Pythagorean theorem, hypotenuse2 = sum of the squares of other two sides.
Step: 5
c2 = a2 + b2
Step: 6
42 = 32 + b2
  [Substitute c = 4 and a = 3.]
Step: 7
16 = 9 + b2
Step: 8
b2 = 16 - 9
  [Subtract 9 from both the sides.]
Step: 9
b2 = 7
Step: 10
b = 7
Step: 11
The length of the other side = 7 ft.
Correct Answer is :   7 ft
Q10Jim walked diagonally across a square garden with each side measuring 25 ft in length (from one corner to the opposite corner). How far did he walk?
A. 35.47 ft
B. 33.23 ft
C. 35.35 ft
D. 37.47 ft

Solutions
Share 
Step: 1
Let s be the side of the square garden and d be the distance Jim walked.
Step: 2
All the angles of a square are right angles. So, the diagonal of the square will be the hypotenuse of the right triangle formed by two adjacent sides and the diagonal.
Step: 3
d2 = s2 + s2
  [Apply Pythagorean theorem.]
Step: 4
d2 = 252 + 252
  [Substitute s = 25.]
Step: 5
d2 = 625 + 625 = 1250
  [Apply exponents and simplify.]
Step: 6
d = √1250 = 35.35
  [Take square root on both sides.]
Step: 7
The total distance Jim walked is 35.35 ft.
Correct Answer is :   35.35 ft
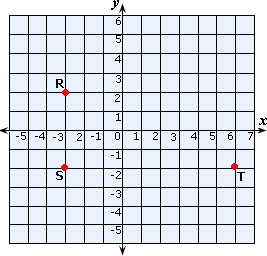
Q11The points R(- 3, 2), S(- 3, - 2) and T(6, - 2) represents the positions of Andrew, Roger and Peter respectively, playing in a playground. Find the distance between Andrew and Peter.


A. 9 units
B. 9.85 units
C. 10 units
D. 8.75 units

Solutions
Share 
Step: 1
Plot the points R(- 3, 2), S(- 3, - 2) and T(6, - 2) in a Cartesian plane and join them.
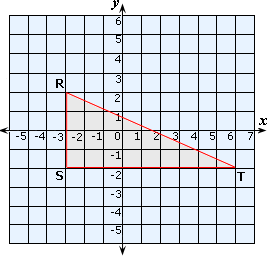
Step: 2
Distance between the point R and the point S = 2 - (-2) = 4 units
  [Difference between the y-coordinates.]
Step: 3
Distance between the point S and the point T = 6 - (-3) = 9 units
  [Difference between the x-coordinates.]
Step: 4
Distance between Andrew and Peter = Distance between the point R and the point T
Step: 5
Since ΔRST is a right-angled triangle,
RT2 = RS2 + ST2
  [Pythagoras′ theorem.]
Step: 6
RT2 = 42 + 92
  [Substitute the values.]
Step: 7
RT2 = 16 + 81 = 97
  [Add.]
Step: 8
RT = 97 = 9.85 units
  [Take square root on both sides.]
Step: 9
Therefore, the distance between Andrew and Peter is 9.85 units.
Correct Answer is :   9.85 units
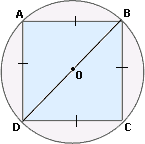
Q12The radius of the circle is 5 in. Find the length of the sides of the square.


A. 52 in.
B. 10 in.
C. 5 in.
D. 102 in.

Solutions
Share 
Step: 1
The radius of the circle OB = 5 in.
Step: 2
Diameter of the circle, BD = 10 in.
  [diameter = 2 × radius.]
Step: 3
From right triangle BDC, BD2 = BC2 + CD2
  [Apply Pythagorean theorem.]
Step: 4
BD2 = BC2 + BC2
  [Since all sides of a square are equal,replace CD with BC.]
Step: 5
102 = 2BC2
  [Substitute BD.]
Step: 6
100 = 2BC2
  [Simplify.]
Step: 7
BC2 = 1002 = 50
  [Divide by 2 on both sides.]
Step: 8
BC = 50 = 52
  [Take square root of both sides.]
Step: 9
The length of side of square = 52 in.
Correct Answer is :   52 in.
Q13The perimeter of a right triangle is 210 inches and the ratio of the lengths of the 2 legs is 5 : 12. Find the length of the hypotenuse.

A. 91 inches
B. 84 inches
C. 35 inches
D. None of the above

Solutions
Share 
Step: 1
The two legs of a right triangle are in the ratio 5:12
Step: 2
Let the length of two legs be 5k and 12k respectively.
Step: 3
Hypotenuse2 = (5k)2 + (12k)2
  [Apply Pythagorean theorem.]
Step: 4
Hypotenuse2 = 25k2 + 144k2
  [Apply exponents .]
Step: 5
= 169k2
  [Simplify.]
Step: 6
Hypotenuse = 169k2 = 13k
  [Take square root of both sides.]
Step: 7
The perimeter of right triangle = 210 inches.
Step: 8
Perimeter of the right triangle = 5k + 12k + 13k = 30k.
Step: 9
30k = 210
  [Equate perimeters]
Step: 10
k = 21030 = 7
  [Divide by 30 on both sides.]
Step: 11
Hypotenuse = 13k = 13 × 7 = 91
  [Substitute k.]
Step: 12
The length of hypotenuse = 91 inches.
Correct Answer is :   91 inches
Q14The lengths of hypotenuse and shorter leg of a right triangle are in the ratio 5 : 3 and the perimeter of the triangle 36 inches. Find the length of the longer leg.

A. 12 inches
B. 9 inches
C. 18 inches
D. 4 inches

Solutions
Share 
Step: 1
The lengths of hypotenuse and shorter leg of a right triangle are in the ratio 5:3
Step: 2
Let the length of hypotenuse and shorter leg be 5k and 3k respectively.
Step: 3
Let the length of longer leg be x.
Step: 4
x2 = (5k)2 - (3k)2
  [Apply Pythagorean theorem.]
Step: 5
x2 = 25k2 - 9k2
  [Evaluate powers.]
Step: 6
x = 16k2 = 4k
  [Subtract and find the positive square root.]
Step: 7
The perimeter of triangle = 36 inches.
Step: 8
Perimeter of the right triangle = 5k + 4k + 3k = 12k.
Step: 9
12k = 36
  
Step: 10
k = 3612= 3
  [Divide both sides with 12 and simplify.]
Step: 11
The length of longer leg = 4k = 4 × 3 = 12 inches.
Correct Answer is :   12 inches
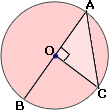
Q15Diameter of the circle O is 34 cm. Find the length of the chord AC.


A. 17 cm
B. 172 cm
C. 342 cm
D. 217 cm

Solutions
Share 
Step: 1
The diameter of the circle O = 34 cm = AB
Step: 2
Radius of the circle OA = OC = 342 = 17 cm
  [Radius = Diameter2 .]
Step: 3
OAC is a right triangle.
Step: 4
AC2 = OA2 + OC2
  [Apply Pythagorean theorem]
Step: 5
AC2 = (17)2 + (17)2
  [Replace OA and OC with 17.]
Step: 6
AC2 = 289 + 289 = 578
  [Apply exponents and simplify.]
Step: 7
AC = 578 = 172
  [Find the positive square root.]
Step: 8
The length of the chord AC = 172 cm.
Correct Answer is :    172 cm

HighSchool Math