Solved Examples and Worksheet for Areas of Composite Plane Figures

Q1Find the area of the figure.


A. 22 m2
B. 18 m2
C. 25 m2
D. 16 m2

Solutions
Share 
Step: 1
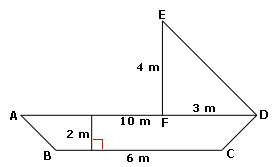
The area of the figure = Area of the trapezoid ABCD + Area of the Δ DEF.
Step: 2
The area of the trapezoid ABCD = 12 x height x (sum of the measures of the parallel sides)
Step: 3
= 12 x height x (AD + BC)
  
Step: 4
= 12 x 2 x (10 + 6)
  [Substitute AD = 10 m, BC = 6 m and height = 2 m.]
Step: 5
= 12 x 2 x 16 = 16 m2
  [Simplify.]
Step: 6
= 16 m2
  [Simplify.]
Step: 7
The area of ΔDEF= 12 x base x height = 12 x FD x EF
Step: 8
= 12 x 3 x 4
  [Substitute FD = 3 m and EF = 4 m.]
Step: 9
= 122 = 6 m2
  [Simplify.]
Step: 10
So, area of the figure = 16 + 6 = 22 m2
  [Substitute the values.]
Correct Answer is :   22 m2
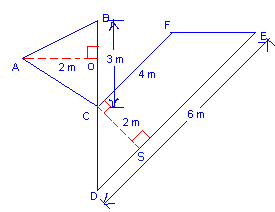
Q2What is the total area of the figure? [Assume that CDEF is a trapezoid.]


A. 5 m2
B. 12 m2
C. 13 m2
D. None of the above

Solutions
Share 
Step: 1
The total area of the figure = area of the triangle ABC + area of the trapezoid CDEF.
Step: 2
The area of the triangle ABC = 12 × base × height
Step: 3
= (12) × BC × AO
  
Step: 4
= (12) × 3 × 2
  [Substitute BC = 3 m and AO = 2 m.]
Step: 5
= 3 m 2
  [Simplify.]
Step: 6
The area of the trapezoid CDEF = (12) × height × (sum of the measures of the parallel sides)
Step: 7
= (12) × CS × (CF + DE)
  
Step: 8
= (12) × 2 × (4 + 6)
  [Substitute CS = 2, CF = 4 and DE = 6.]
Step: 9
= (12) × 2 × 10
  [Work inside the grouping symbols.]
Step: 10
= 10 m2
  [Simplify.]
Step: 11
The total area of the figure = 3 + 10 = 13 m2.
  [Substitute the values.]
Correct Answer is :   13 m2
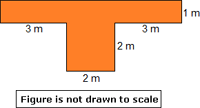
Q3Find the area of the figure ABCDE if the area of ABCE is 40 cm2 and area of ECD is 20 cm2.

A. 40 cm2
B. 60 cm2
C. 20 cm2
D. 80 cm2

Solutions
Share 
Step: 1
In the given figure, the area of ABCE is 40 cm2 and the area of ECD is 20 cm2.
  [Given.]
Step: 2
The area of ABCDE = area of ABCE - area of ECD
  [From the given figure.]
Step: 3
= 40 - 20
  [From step 1.]
Step: 4
= 20
  [Subtract.]
Step: 5
Therefore, the area of the given figure ABCDE is 20 cm2 .
Correct Answer is :   20 cm2
Q4Find the area of rectangle ABCD, if the area of the triangle ABC is 12 cm 2.

A. 24 cm.2
B. 28 cm.2
C. 12 cm.2
D. 16 cm.2

Solutions
Share 
Step: 1
Diagonal AC divides the rectangle into two congruent triangles.
Step: 2
Area of the triangle ABC = 12 cm2.
Step: 3
Area of the rectangle ABCD = 2 × area of traingle ABC.
= 2 × 12
  
Step: 4
So, the area of the rectangle ABCD = 24 cm2.
Correct Answer is :   24 cm.2
Q5Find the area of the figure.


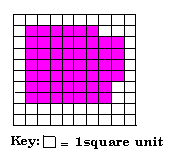
A. 56 square units
B. 48 square units
C. 44 square units
D. 52 square units

Solutions
Share 
Step: 1
In the given figure, 52 squares are colored.
Step: 2
Area of each square = 1 square unit.
Step: 3
Area of 52 squares = 52 × 1 = 52 square units.
Correct Answer is :   52 square units
Q6Find the area of the figure.


A. 38 yd2
B. 27 yd
C. 38 yd
D. 32 yd2

Solutions
Share 
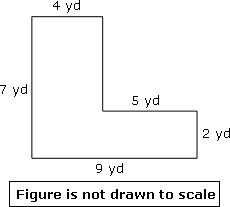
Step: 1

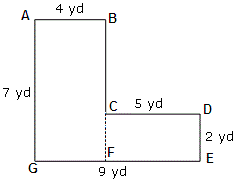
Step: 2
From the figure, Area of the rectangle ABFG = length × width = AG × AB = 7 × 4 = 28 sq.yd
Step: 3
Area of the rectangle CDEF = length × width = CD × DE = 5 × 2 = 10 sq.yd
Step: 4
Total area of the figure ABCDEFG = area of the rectangle ABFG + area of the rectangle CDEF
Step: 5
= 28 + 10 = 38
Step: 6
So, total area = 38 sq.yd
Correct Answer is :   38 yd2
Q7Find the area of the figure.

A. 88 sq ft
B. 69 sq ft
C. 108 sq ft
D. 105 sq ft

Solutions
Share 
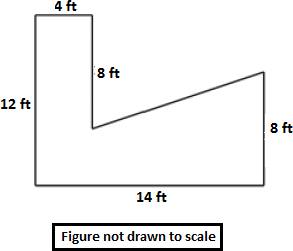
Step: 1
Label the given figure as shown below and draw line EH perpendicular to DF.
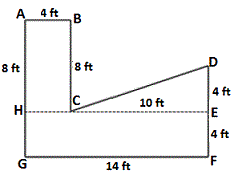
Step: 2
Area of rectangle ABCH = 8 × 4 = 32 sq ft.
  [Area of rectangle = length × width.]
Step: 3
Area of triangle CDE = 12 × 10 × 4 = 20 sq ft.
  [Area of triangle = 12 × base × height.]
Step: 4
Area of rectangle EFGH = 14 × 4 = 56 sq ft.
  [Area of rectangle = length × width.]
Step: 5
The total area of the given figure ABCDEFGH = Area of rectangle ABCH + Area of triangle CDE + Area of rectangle EFGH.
Step: 6
= 32 + 20 + 56
  [From steps 2, 3, and 4.]
Step: 7
= 108
  [Add.]
Step: 8
Therefore, the total area of the given figure is 108 sq ft.
Correct Answer is :   108 sq ft
Q8Find the area of the figure.

A. 90 cm2
B. 66 cm2
C. 80 cm2
D. 137 cm2

Solutions
Share 
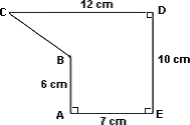
Step: 1
  [Draw BF¯ ⊥ ED¯.]

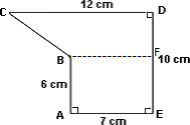
Step: 2
ABFE is a rectangle in which AB = EF = 6 cm and AE = BF = 7 cm. BCDF is a trapezium in which CD = 12 cm, BF = 7 cm and DF = 4 cm as shown.
Step: 3
Area of rectangle ABFE = 7 × 6 = 42 cm2
  [Area of a rectangle = length × width.]
Step: 4
Area of trapezoid = ( 12)(4)(7 + 12) = 38 cm2
  [Area of trapezoid = 12 h (b1 + b2).]
Step: 5
Total area of the figure = 42 + 38 = 80 cm2
Correct Answer is :   80 cm2
Q9Find the area of the figure shown.


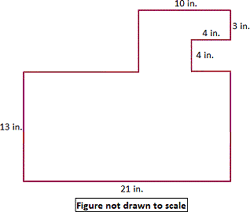
A. 363 sq in
B. 399 sq in.
C. 360 sq in
D. 327 sq in.

Solutions
Share 
Step: 1

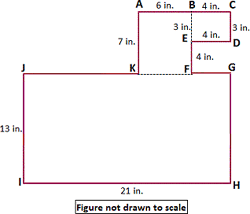
Step: 2
The given figure is divided into 3 rectangles.
Step: 3
Area of rectangle = length × width.
Step: 4
Area of rectangle ABFK = 7 × 6 = 42 sq in.
Step: 5
Area of rectangle BCDE = 4 × 3 = 12 sq in.
Step: 6
Area of rectangle GHIJ = 21 × 13 = 273 sq in.
Step: 7
Total area of the given figure ABCDEHGHIJK = Area of rectangle ABFK + Area of rectangle BCDE + Area of rectangle GHIJ.
Step: 8
= 42 + 12 + 273
  [From steps 4, 5, and 6.]
Step: 9
= 327
  [Add.]
Step: 10
Therefore, the total area of the given figure is 327 sq in.
Correct Answer is :   327 sq in.
Q10Find the area of the figure.


A. 116 cm2
B. 108 cm2
C. 36 cm2
D. 68 cm2

Solutions
Share 
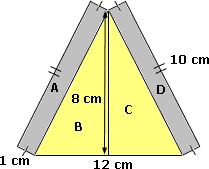
Step: 1
Area of the figure = Area of A + Area of B + Area of C + Area of D
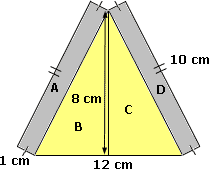
Step: 2
Area of A = Area of D
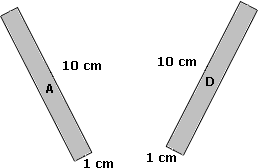
  [The dimensions of A and D are the same.]

Step: 3
Area of A = Area of D = 1 cm × 10 cm = 10 cm2
  [Area of a rectangle = length × width.]
Step: 4
Area of B = Area of C
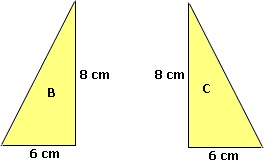
  [The dimensions of B and C are the same.]

Step: 5
Area of B = Area of C = 12 × 6 cm × 8 cm = 24 cm2
  [Area of a triangle = 12 × base × height.]
Step: 6
Area of the figure = 10 cm2 + 24 cm2 + 24 cm2 + 10 cm2
  [Substitute the values.]
Step: 7
= 68 cm2
  [Add.]
Step: 8
Therefore, area of the figure is 68 cm2.
Correct Answer is :   68 cm2
Q11Find the area of the composite shape.

A. 149 cm2
B. 172 cm2
C. 151 cm2
D. 163 cm2

Solutions
Share 
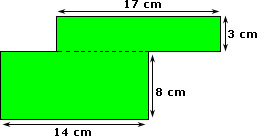
Step: 1
The area of a composite 2-D shape can be found by finding the areas of individual shape and adding them up.
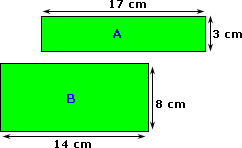
Step: 2
Area = Length × Width
Step: 3
Area A = 17 × 3 = 51 cm2
Step: 4
Area B = 14 × 8 = 112 cm2
Step: 5
Total area = 51 cm2 + 112 cm2 = 163 cm2
Step: 6
So, the area of the given composite shape is 163 cm2.
Correct Answer is :   163 cm2
Q12Find the area of the composite shape.

A. 82 cm2
B. 76 cm2
C. 65 cm2
D. 56 cm2

Solutions
Share 
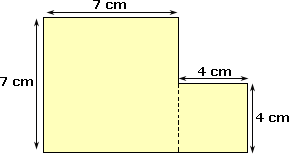
Step: 1
The area of a composite 2-D shape can be found by finding the areas of individual shape and adding them up.
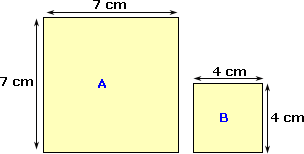
Step: 2
Area = Length × Width
Step: 3
Area A = 7 × 7 = 49 cm2
Step: 4
Area B = 4 × 4 = 16 cm2
Step: 5
Total area = 49 cm2 + 16 cm2 = 65 cm2
Step: 6
So, the area of the given composite shape is 65 cm2.
Correct Answer is :   65 cm2
Q13Find the area of the figure shown.

A. 111 m2
B. 160 m2
C. 133 m2
D. 153 m2

Solutions
Share 
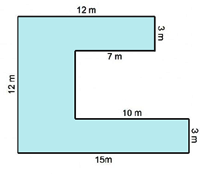
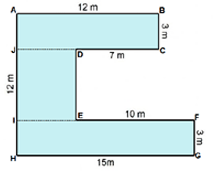
Step: 1
The figure is divided into three rectangles.
Step: 2

Step: 3
Area of the figure = Area of rectangle ABCJ + Area of rectangle DEIJ + Area of rectangle FGHI
Step: 4
= AB × BC + JD × DE + IF × FG
Step: 5
= 12 × 3 + 5 × 6 + 15 × 3
Step: 6
= 36 + 30 + 45 = 111
Step: 7
Therefore, area of the figure is 111 m2.
Correct Answer is :   111 m2
Q14Find the area of the figure shown.

A. 66 m2
B. 53 m2
C. 50 m2
D. 75 m2

Solutions
Share 
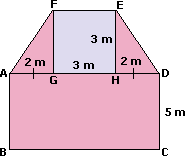
Step: 1
Area of the figure = Area of trapezium FADE + Area of rectangle ABCD
Step: 2
= 12 × FG × (FE + AD) + AD × CD
Step: 3
= 12 × 3 × (3 + 7) + 7 × 5
Step: 4
= 15 + 35 = 50
Step: 5
Therefore, area of the figure is 50 m2.
Correct Answer is :   50 m2
Q15Find the area of the figure.

A. 14 m2
B. 11 m2
C. 10 m2
D. 12 m2

Solutions
Share 
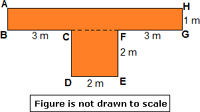
Step: 1
The figure is divided into a square and a rectangle.
Step: 2
Area of the figure = Area of square CDEF + Area of rectangle ABGH
Step: 3
= DE × EF + AH × GH
  [Area of rectangle = length × width, and Area of square = side × side.]
Step: 4
= 2 × 2 + 8 × 1 = 4 + 8 = 12
Step: 5
Therefore, area of the figure is 12 m2.
Correct Answer is :   12 m2

HighSchool Math