Solved Examples and Worksheet for Representing Distributive Property Using Area Models
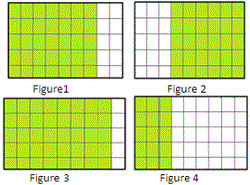
A. Figure 1
B. Figure 3
C. Figure 2
D. Figure 4
Step: 1
In Figure 2, the rectangle is the combined figure of 2 rectangles and the area = (5 × 3) + (5 × 6) = 5(3 + 6).
Step: 2
In Figure 3, the rectangle is the combined figure of 2 rectangles and the area = (5 × 8) + (5 × 1) = 5(8 + 1).
Step: 3
In Figure 4, the rectangle is the combined figure of 2 rectangles and the area= (5 × 3) + (5 × 6) = 5(3 + 6).
Step: 4
In Figure 1, the rectangle is the combined figure of 2 rectangles and the area 5(7 + 2) = (5 × 7) + (5 × 2) .
Step: 5
Therefore the correct answer is Figure 1.
Correct Answer is : Figure 1
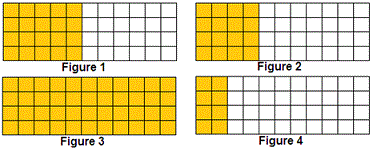
A. Figure 2
B. Figure 3
C. Figure 4
D. Figure 1
Step: 1
Figure 2 is the combined figure of 2 rectangles and the area = (4 × 4) + (4 × 7) = 4(4 + 7).
Step: 2
Figure 3 will not hold distributive property as it is not a combined rectangle.
Step: 3
Figure 4 is the combined figure of 2 rectangles and the area = (4 × 2) + (4 × 9) = 4(2 + 9).
Step: 4
Figure 1 is the combined figure of 2 rectangles and the area = (4 × 5) + (4 × 6) = 4(5 + 6).
Step: 5
Therefore the correct answer is figure 1.
Correct Answer is : Figure 1

A. 3(7 + 2)
B. (7 × 3 ) + (7 × 3)
C. 7(3 + 2)
D. 2(3 + 7)
Step: 1
The areas of each rectangle in the pair of given rectangles = (3 × 7) and (3 × 2)
Step: 2
When we pair up both the rectangles the figure will be as shown below.
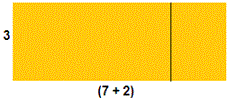
[Using distributive Property.]
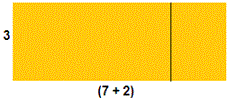
Step: 3
Therefore area = 3(7 + 2).
Step: 4
The total area of the new rectangle formed is the same as the sum of the areas of each individual rectangle.
Step: 5
That means, (3 × 7) + (3 × 2) = 3(7 + 2).
Correct Answer is : 3(7 + 2)
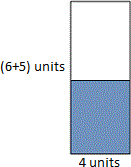
A. 30 square units
B. 20 square units
C. 25 sq units
D. 24 square units
Step: 1
We can divide the given figure into two rectangles. We find that one is shaded and the other is unshaded.
[By using distributive Property.]

Step: 2
Here 4 × 6 is the area of plain rectangle, 4 × 5 is the area of the colored rectangle.
[One of the dimensions is same for both the rectangles.]
Step: 3
Therefore the area of plain rectangle = 4 × 6 = 24 square units.
Correct Answer is : 24 square units
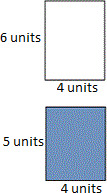
A. 6 sq units
B. 12 sq units
C. 7 sq units
D. 8 sq units
Step: 1
We can divide the given figure into two rectangles. We find that one is shaded and the other is unshaded.
[By using distributive Property.]

Step: 2
Here 2 × 4 is the area of colored rectangle, 2 × 3 is the area of the plain rectangle.
[One of the dimensions is same for both the rectangles.]
Step: 3
Therefore the area of plain rectangle = 2 × 3 = 6 square units.
Correct Answer is : 6 sq units
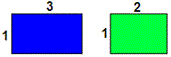
A. 1(3 + 2)
B. 2(1 + 3)
C. (2 × 1) + (2 ×32)
D. 3(1 + 2)
Step: 1
The areas of each rectangle in the pair of given rectangles are (1 × 3) and (1 × 2).
Step: 2
Sum up the given rectangles shown below.
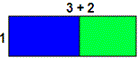
[Using distributive Property.]

Step: 3
Therefore total area = 1 × (3 + 2).
Step: 4
The total area of pair of rectangles is same as the sum of the areas of each individual rectangles.
Step: 5
That means, (1 × 3) + (1 × 2) = 1(3 + 2).
Correct Answer is : 1(3 + 2)

A. (4 × 3) + (4 × 7)
B. 4(3 + 7)
C. 3(4 + 7)
D. 7(4 + 3)
Step: 1
The areas of each rectangle in the pair of given rectangles are (3 × 4) and (3 × 7).
Step: 2
Sum up the rectangles as given below.

[Using distributive Property.]

Step: 3
Therefore the total area = 3 × (4 + 7).
Step: 4
The total area of pair of rectangles is same as the sum of areas of each individual rectangles.
Step: 5
That means, (3 × 4) + (3 × 7) = 3(4 + 7).
Correct Answer is : 7(4 + 3)
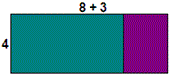
A. (8 × 3) + (8 × 4)
B. 4(8 + 4)
C. (4 × 8) + (4 × 3)
D. 3(8 + 4)
Step: 1
The area of the rectangle from the given figure = 4 × (8 + 3).
Step: 2
To calculate the areas of each rectangle, decompose the given rectangle as shown below.
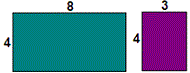
[One of the dimensions is same for both the rectangles.]

Step: 3
Now, the areas are (4 × 8) and (4 × 3).
[Using distributive Property.]
Step: 4
Sum up the two areas to get the total area of the figure.
Step: 5
That is (4 × 8) + (4 × 3) = 4(8 + 3).
Correct Answer is : (4 × 8) + (4 × 3)
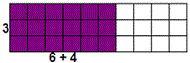
A. 3 × 4
B. (6 × 4) + (6 × 3)
C. 3(6 + 4)
D. 3 × 6
Step: 1
Area of the given figure = 3(6 + 4) = (3 × 6) + (3 × 4)
[By Distributive property.]
Step: 2
We can divide the given figure into two rectangles. We find that one rectangle is shaded and the other is not shaded.
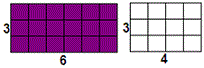
[One of the dimensions is same for both the rectangles.]

Step: 3
Area of the shaded rectangle from the above figure is 3 × 6 and the area of the unshaded rectangle is 3 × 4.
Step: 4
Therefore the area of shaded rectangle = 3 × 6.
Correct Answer is : 3 × 6
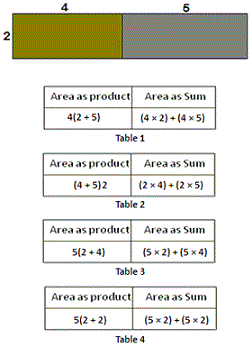
A. Table 4
B. Table 3
C. Table 1
D. Table 2
Step: 1
From the given figure, width of the rectangle is 2 units and the length of the rectangle is (4 + 5).
Step: 2
The area of a rectangle is the product of its length and width.
Step: 3
So the area as product = (4 + 5) 2
Step: 4
Now, decompose the given rectangle into two rectangles as shown below.

[Using distributive Property.]

Step: 5
To find the area as sum, calculate the area of each rectangle and sum the areas.
Step: 6
That means, area as sum = (2 × 4) + (2 × 5)
[One of the dimensions is same for both the rectangles.]
Correct Answer is : Table 2
- Telling Time to the nearest Minute-Gr 3-Solved Examples
- Elapsed Time-Gr 3-Solved Examples
- Measuring Length Using Ruler-Gr 3-Solved Examples
- Estimating Metric Units-Gr 3-Solved Examples
- Using Operations to Solve Problems Involving Volume and Mass-Gr 3-Solved Examples
- Perimeter of Polygons-Gr 3-Solved Examples
- Finding an Unknown Dimension of a Polygon-Gr 3-Solved Examples
- Finding Area of Rectangles by Tiling-Gr 3-Solved Examples
- Area of Plane Figures - Counting Unit Squares-Gr 3-Solved Examples
- Finding Areas of Rectilinear Figures-Gr 3-Solved Examples
- Solving Problems on Area of Rectangles-Gr 3-Solved Examples
- Rectangles with Same Area but Different Perimeters and Same Perimeter but Different Areas-Gr 3-Solved Examples
- Constructing Pictographs-Gr 3-Solved Examples
- Constructing Bar Graphs-Gr 3-Solved Examples
- Interpreting Bar Graphs-Gr 3-Solved Examples
Related Worksheet
- Distributive Property