Vector Multiplication
Definition Of Vector Multiplication
In Vector Multiplication, a vector is multiplied by one or more vectors or by a scalar quantity
More About Vector Multiplication
There are three different types of multiplication: dot product, cross product, and multiplication of vector by a scalar
The dot product of two vectors u and v is given as u . v = uv cos θ where θ is the angle between the vectors u and v
The cross product of two vectors u and v is given as u × v = uv sin θ where θ is the angle between the vectors u and v
When a vector is multiplied by a scalar, only the magnitude of the vector is changed, but the direction remains the same
Video Examples: Multiplying Vectors
Examples of Vector Multiplication
If the vector 
is multiplied by a scalar then 
If u = 2i + 6j and v = 3i - 4j are two vectors and angle between them is 60°, then to find the dot product of the vectors, we first find their magnitude.
Magnitude of vector 
Magnitude of vector 
The dot product of the vectors u, v is u · v = uv cos θ
= (2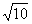
) (5) cos 60°
= (2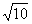) (5) ×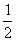 
= 5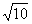
If u = 5i + 12j and v = 3i + 6j are two vectors and angle between them is 60°, then to find the cross product of the vectors, we first find their magnitude.
Magnitude of vector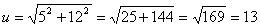 
Magnitude of vector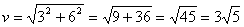 
The cross product of the vectors u, v is u × v = uv sin θ
Solved Example on Vector Multiplication
Ques: Which of the following is the dot product of the vectors u = 6i + 8j and v = 7i - 9j?
Choices:
A. 114
B. - 30
C. - 2
D. 110
Correct Answer: B
Solution:
Step 1: u = 6i + 8j, v = 7i - 9j are the two vectors
Step 2: Dot product of the two vectors u, v = u . v = u1v1 + u2v2
Step 3: = (6i + 8j) . (7i - 9j)
Step 4: = (6) (7) + (8) (- 9) [Use the definition of the dot product of two vectors.]
Step 5: = - 30 [Simplify.]