One-To-One Function
Definition Of One To One Function
A function is said to be a One-to-One Function, if for each element of range, there is a unique domain.
More About One to One Function
One-to-one function satisfies both vertical line test as well as horizontal line test.
One-to-one function is also called as injective function.
Example of One to One Function
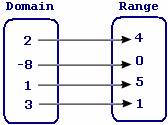
In the given figure, every element of range has unique domain.
So, the given function is one-to-one function.
Video Examples: One-to-one Functions
Solved Example on One to One Function
Ques: Let A = {1, 2, 3} and B = {a, b, c, d}. Which of the following is a one-to-one function?
Choices:
A. {(1, a), (2, c), (3, a)}
B. {(1, b), (2, d), (3, a)}
C. {(1, a), (2, a), (3, a)}
D. {(1, c), (2, b), (1, a), (3, d)}
Correct Answer: B
Solution:
Step 1: Here, option B satisfies the condition for one-to-one function, as the elements of the range set B are mapped to unique element in the domain set A and the mapping can be shown as:
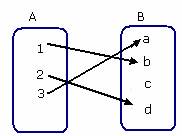
Step 2: Hence Option B satisfies the condition for a function to be one-to-one.