Indirect Proof
Definition Of Indirect Proof
Indirect proof is a type of proof in which a statement to be proved is assumed false and if the assumption leads to an impossibility, then the statement assumed false has been proved to be true
Video Examples: Introduction to Indirect Proof
Example of Indirect Proof
Sum of 2n even numbers is even, where n > 0. Prove the statement using an indirect proof.
The first step of an indirect proof is to assume that 'Sum of even integers is odd.'
That is, 2 + 4 + 6 + 8 + . . . .+ 2n = an odd number
⇒ 2(1 + 2 + 3 + 4 + . . . + n) = an odd number ⇒ 2 ×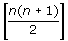 
= an odd number
⇒ n(n + 1) = an odd number, a contradiction, because n(n + 1) is always an even number.
Thus, the statement is proved using an indirect proof.
Solved Example on Indirect Proof
Ques: Prove the following statement using an indirect proof: â–³LMN has at most one right angle.
Solution:
Step 1: Assume â–³LMN has more than one right angle. That is, assume that angle L and angle M are both right angles.
Step 2: If M and N are both right angles, then m∠L = m∠M = 90
Step 3: m∠L + m∠M + m∠N = 180 [The sum of the measures of the angles of a triangle is 180.]
Step 4: Substitution gives 90 + 90 + m∠N = 180.
Step 5: Solving gives m∠N = 0.
Step 6: This means that there is no â–³LMN, which contradicts the given statement.
Step 7: So, the assumption that ∠L and ∠M are both right angles must be false.
Step 8: Therefore, â–³LMN has at most one right angle.