Incenter
Definition Of Incenter
Incenter is the center of a circle inscribed in a triangle. It is the point of intersection of all the angle bisectors of a triangle.
More About incenter
Incenter of a triangle is equidistant from the sides of the triangle. The Cartesian coordinates of the incenter, with the vertices of the triangle being ,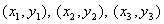
and lengths of the opposite sides of the triangle being a, b, and c, are given by 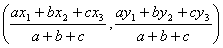 .
.
Video Examples:Incenter and incircles of a triangle
Example of incenter
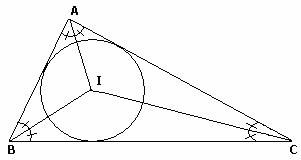
The incenter for the above figure is "I" as it is the center of the circle inscribed in a triangle.So, "I" is the incenter for the above figure.
Solved Example on incenter
Ques: Select the correct statements.
I. The triangle is inscribed in the circle.
II. I is called incenter.
III. Angle ABI is always equal to Angle BAI.
IV. BI is called inradius.
Choices:
A. Only IV
B. I and II
C. Only II
D. I and IV
Correct Answer: C
Solution:
Step 1: Here, 'I is called incenter' is the only correct statement.
[The point of concurrency of the three angle bisectors of a triangle is called the incenter.]