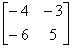IDENTITY MATRIX
Definition Of Identity Matrix
A square matrix in which all the main diagonal elements are 1's and all the remaining elements are 0's is called an Identity Matrix.
More About Identity Matrix
Identity Matrix is also called as Unit Matrix or Elementary Matrix.
Identity Matrix is denoted with the letter "In×n", where n×n represents the order of the matrix.
One of the important properties of identity matrix is: A×In×n = A, where A is any square matrix of order n×n.
Video Examples: The Identity Matrix
Example of Identity Matrix
are identity matrices of order 1×1, 2×2, 3×3,....n×n.
Solved Example on Identity Matrix
Ques: If M =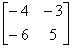
, then find M×I, where I is an identity matrix.
Choices:
Correct Answer: B
Solution:
Step 1: M = 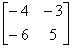[Given.]
Step 2: As M is square matrix of order 2×2, the identity matrix I is also of same order 2×2. [Rule for Matrix Multiplication.]
Step 3: Then M×I = ×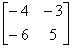 
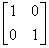[Matrix Multiplication.]
Step 4: = 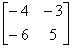[Simplifying.]
Step 5: Hence M×I = M =
Quick Summary
- Also called Unit Matrix or Elementary Matrix.
- Denoted as In×n, where n×n represents the order of the matrix.
- A × In×n = A, where A is any square matrix of order n×n.
🍎 Teacher Insights
Emphasize the role of the identity matrix as the multiplicative identity. Use examples to illustrate its application in simplifying matrix expressions and solving linear systems. Show visual representations to help students understand the structure of the identity matrix.🎓 Prerequisites
- Matrix
- Square Matrix
- Matrix Multiplication
Check Your Knowledge
Q1: Which of the following is an Identity Matrix?
Q2: If A is a 3x3 matrix, what is A * I where I is a 3x3 identity matrix?
Frequently Asked Questions
Q: What is the importance of the Identity Matrix?
A: It acts as the multiplicative identity in matrix algebra, similar to how 1 functions in scalar multiplication.
Q: Can an Identity Matrix be rectangular?
A: No, it must be a square matrix.