Circumcenter
Definition Of Circumcenter
Circumcenter of a triangle is the point of intersection of all the three perpendicular bisectors of the triangle.
More About Circumcenter
The circle drawn around the triangle by taking circumcenter as the center is called a circumscribed circle.
Video Examples: Circumcenters
Example of Circumcenter
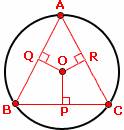
In the above diagram, the three perpendicular bisectors PO, QO, and RO of sides BC, AB, and AC of the triangle ABC intersect at the point O. So, the point O is called the circumcenter of the triangle ABC.
Solved Example on Circumcenter
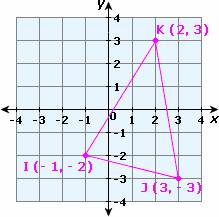
Ques: Find the circumcenter of the triangle in the figure shown.
Choices:
A. (-73/46,-7/46)
B. (73/46,7/46)
C. (73/46,-7/46)
D. (-73/46,7/46)
Correct Answer: C
Solution:
Step 1: The point where all the perpendicular bisectors intersect is called circumcenter.
Step 2: To find the perpendicular bisector of , find the midpoint of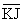 
and then find its slope.
Step 3: Midpoint of 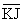is ((2+3)/2,(3-3)/2 ) = (5/2, 0)
Step 4: Slope of 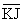is - 6
Step 5: The slope of perpendicular bisector of 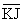is the negative reciprocal of - 6,1/6
Step 6: The perpendicular bisector of 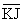passes through the midpoint of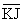
Step 7: So, the equation of perpendicular bisector of 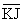is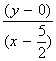
= 1/6 implies 2x - 12y = 5.
Step 8: Similarly, the equation of perpendicular bisector of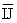 
is 8x - 2y = 13.
Step 9: Solving 2x - 12y = 5 and 8x - 2y = 13 gives x =73/46 and y = -7/46 .
Step 10: So the circumcenter of the given triangle is (73/46, -7/46 )