Parabola
Definition Of Parabola
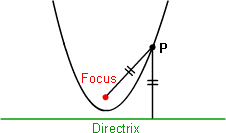
A parabola is the set of all points in a plane that are equidistant from the focus and the directrix of the parabola.
More About Parabola
The graph of any quadratic equation is a parabola.
All parabolas have an axis of symmetry and the point at which the axis of symmetry intersects the parabola is called the vertex of the parabola and the vertex lies half way between the focus and the directrix.
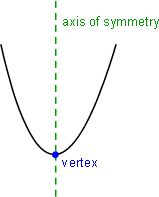
Directrix is a line that is perpendicular to the axis of symmetry of a parabola.
Focus of a parabola lies on the axis of symmetry.
Video Examples: Free Math Lessons Parabolas
Solved Example on Parabola
Ques: Find the equation of the parabola shown.
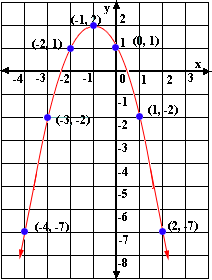
Choices:
A. y = x3 + 2x + 1
B. y = - x2 + 2x3 + 1
C. y = x2 - 2x + 1
D. y = - x2 - 2x + 1
Correct Answer: D
Solution:
Step 1: The equation of a parabola is of the form: y = ax2 + bx + c.
Step 2: Substitute any 3 ordered pairs that lie on the parabola shown into the quadratic equation in step 1.
Step 3: Solve the three equations formed to get the values of a, b, and c.
Step 4: Substitue the values of a, b, and c in the original quadratic equation in step 1. Therefore the equation of the parabola is y = - x2 - 2x + 1.
Real-world Connections
The graph that models the motion of a falling object is of the shape of a parabola.
The graph that models the path of a baseball hit by a player is a parabola.