Orthocenter
Definition of Orthocenter
The point of intersection of the altitudes of a triangle is called an orthocenter.
More about Orthocenter
Orthocenter of an obtuse triangle lies outside the triangle.
Orthocenter of an acute triangle lies inside the triangle.
Orthocenter of a right triangle lies on the triangle.
Example of Orthocenter
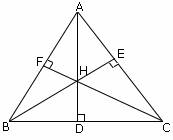
In the figure, AD, BE, and CF are the altitudes drawn from the vertices A, B, and C respectively. The point of intersection of these altitudes is 'H'. So, 'H' is the orthocenter of the triangle ABC.
Solved Example on Orthocenter
In a right-angled triangle, the orthocenter lies
Choices:
A. at the vertex containing the right angle
B. outside the triangle
C. at the midpoint of the hypotenuse
D. inside the triangle
Correct Answer: A
Solution:
Step 1:
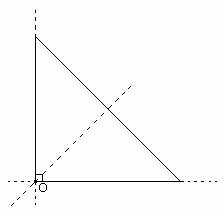
Step 2: Orthocenter is the point of intersection of the altitudes. Each leg in a right triangle forms an altitude.
Step 3: So, in a right-angled triangle, the orthocenter lies at the vertex containing the right angle.
Related Terms for Orthocenter
Altitude
Point of Intersection
Triangle