Definition Of Odd Function

The function f(x) is said to be 'odd' if and only if f(x) is a real-valued function of a real variable x, and f(- x) = - f(x).

More About Odd Function

The graph of an odd function is symmetric with respect to the origin.
The product of two odd functions is even.
The product of an odd function and an even function is odd.

Example of Odd Function

The function f(x) = x³ is an odd function as:
f(- x) = (- x)³ = - x³ = - f(x) 
So, f(- x) = - f(x).

Video Examples: Even and Odd Functions

Solved Example on Odd Function

Ques: If g(t) = sin h (9t), then which of the following is true?

Choices:

A. An odd function
B. An even function
C. Not an odd function
D. Neither an even nor an odd function
Correct Answer: A

Solution:

Step 1:g(t) = sin h (9t) = 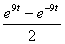 [Formula.]
Step 2:g(- 9t) =  =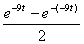 
Step 3: = - (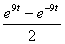) = - g(t)
Step 4: Since g(- t) = - g(t), the given function is an odd function.

Related Worksheet

• Converting-Units-of-Time-Gr-4
• Measuring-Angles---Protractor-Gr-4
• Sum-of-the-Unit-Fractions-Gr-4
• Adding-Mixed-Numbers-Like-Denominators-Gr-4
• Areas-of-Triangles-Gr-6