KITE
Definition Of Kite
A kite is a quadrilateral with two distinct pairs of adjacent sides that are congruent.
More About Kite
A kite has exactly one pair of equal angles
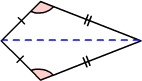
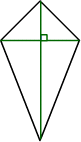
A kite has one line of symmetry.
The diagonals of a kite intersect at right angles
Video Examples: Kite Examples - Geometry
Examples of Kite
The figure below shows a kite.
Solved Example on Kite
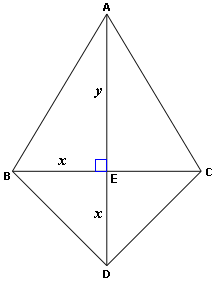
Ques: Find the area of the kite. Measurements shown are in cm. [Given x = 12 and y = 16.]
Choices:
A. 168 cm2
B. 336 cm2
C. 240 cm2
D. 264 cm2
Correct Answer: B
Solution:
Step 1: Triangle ABE is a right triangle. [Diagonals of a kite are perpendicular.]
Step 2: Area of the triangle ABE = 1/2 x 12 x 16 = 96cm2
Step 3: Area of the triangle ACE = Area of the triangle ABE = 96 cm2 [â–³ABE and â–³AEC are congruent triangles.]
Step 4: Triangle BED is a right triangle. [Diagonals of a kite are perpendicular.]
Step 5: Area of the triangle BED =1/2 x 12 x 12 = 72cm2
Step 6: Area of the triangle DEC = Area of the triangle BED = 72 cm2. [Triangle BED and Triangle CED are congruent triangles.]
Step 7: Area of kite = Area of triangle ABE + Area of triangle ACE + Area of triangle BED + Area of the triangle CED = 96 + 96 + 72 + 72 = 336 cm2.