Interior Angle
Definition Of Interior Angle
An Interior Angle of a polygon is the angle formed inside it by any two adjacent sides of the polygon.
When two lines are cut by a third line (transversal), then the angles formed inside the lines are called Interior Angles.
More About Interior Angle
Number of interior angles in a polygon = number of sides of the polygon
Sum of the measures of any interior angle and the corresponding exterior angle in a polygon is 180°.
In a simple polygon, each vertex has one interior angle.
The sum of the measures of all the interior angles of a regular polygon is given by (n - 2) × 180, where n is the number of sides of the regular polygon.
Video Examples: How to Find the Sum of Interior Angles of a Polygon
Example of Interior Angle
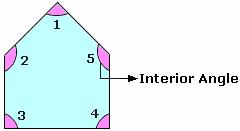
∠1, ∠2, ∠3, ∠4, and ∠5 are the interior angles.
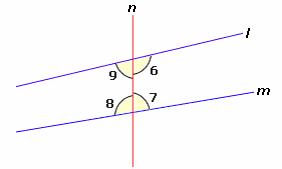∠6, ∠7, ∠8, and ∠9 are the interior angles.
Solved Example on Interior Angle
Ques: Identify the number of interior angles in the figure.
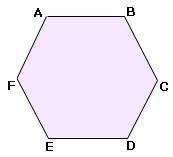
Choices:
A. 4
B. 5
C. 6
D. 7
Correct Answer: C
Solution:
Step 1: The angles formed by joining any two sides of the plane are interior angles.
Step 2: The figure has six sides.
Step 3: So, the number of interior angles is 6. (∠A, ∠B, ∠C, ∠D, ∠E and ∠F are the interior angles.)