Addition Of Vectors
Adding two or more vectors to form a single resultant vector is known as Addition of Vectors.
More about Addition of Vectors
If two vectors have the same direction, then the sum of these two vectors is equal to the sum of their magnitudes, in the same direction.
If the two vectors are in opposite directions, then the resultant of the vectors is the difference of the magnitude of the two vectors and is in the direction of the greater vector.
Examples of Addition of Vectors
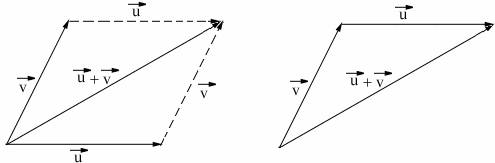
To find the sum of the vectors of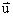 
and,
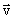they are placed tail to tail to form two adjacent sides of a parallelogram and the diagonal 
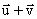gives the sum of the vectors 
and
. This is also called as 'parallelogram rule of vector addition'.
If the vector is represented in Cartesian coordinate, then the sum of the vectors is found by adding the vector components.
The sum of the vectors u = <- 3,="" 4=""> and v = <4, 6=""> is
u + v = <- 3="" +="" 4,="" 4="" +="" 6="">
= <1, 10="">
Video Examples: Addition Of Vectors
Solved Example on Addition of Vectors
Let 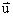= <- 5,8=""> and 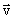= <8, 10="">. Which of the following is the component form of the vector
+ ?
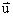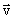Choices:
A. <3, 18="">
B. <18, 13="">
C. <13, 18="">
D. <18, 3="">
Correct Answer: A
Solution:
Step 1: 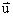= <- 5,="" 8=""> and 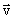= <8, 10="">
Step 2: +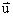
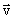
= <- 5,="" 8=""> + <8, 10=""> [Use the definition of sum of vectors.]
Step 3: = <- 5="" +="" 8,="" 8="" +="" 10="">
Step 4: = <3, 18="">